Problem A. 427. (April 2007)

A. 427. We have a sheet of paper with 2007 ``handles'' - long strips, glued to the sheet at the ends. The handles are allowed to cross each other but they are never twisted. Prove that the surface, consisting of the paper sheet and the handles, has at least two boundary loops. (For example, the configuration in the Figure has three boundary loops.)

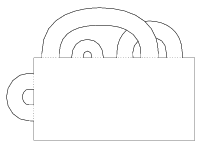
(5 pont)

Deadline expired on May 15, 2007.

Statistics:

7 students sent a solution.
5 points:	Kisfaludi-Bak Sándor, Kornis Kristóf, Lovász László Miklós, Nagy 224 Csaba, Nagy 235 János, Tomon István.
Unfair, not evaluated:	1 solutions.

Problems in Mathematics of KöMaL, April 2007