Problem A. 430. (May 2007)

A. 430. Let n $\ge$ 2 and let $u_1=1,u_2,\ldots,u_n$ be arbitrary complex numbers with absolute values at most 1 and let

f(x)=(x-u₁)(x-u₂)...(x-u_n).

Prove that polynomial f'(x) has a root with a non-negative real part.

(5 pont)

Deadline expired on June 15, 2007.

Solution. If 1 is a multiple root of f then f'(1)=0 and the statement becomes trivial. So we assume that u₂,...,u_n $\ne$ 1.

Let the roots of f'(x) be v₁,v₂...,v_n-1, and consider the polynomial g(x)=f(1-x)=a₁x+a₂x²+...+a_nxⁿ.

The nonzero roots of g(x) are 1-u₂,...,1-u_n. From the Viéta-formulas we obtain

$\sum_{k=2}^m \frac1{1-u_k} = \frac{u_2\ldots u_{n-1}+\ldots+u_3\ldots u_n}{u_2\ldots u_n} = -\frac{a_2}{a_1}.$

The roots of polynomial f'(1-x)=-g'(x)=-a₁-2a₂x-...-na_nx^n-1 are $1-v_1,\ldots,1-v_{n-1}$ ; from the Viéta formulas again,

$\sum_{\ell=1}^{n-1} \frac1{1-v_\ell} = \frac{v_1\ldots v_{n-2}+\ldots+v_2\ldots v_{n-1}}{v_1\ldots v_{n-1}} = -\frac{2a_2}{a_1}.$

Combining the two equations,

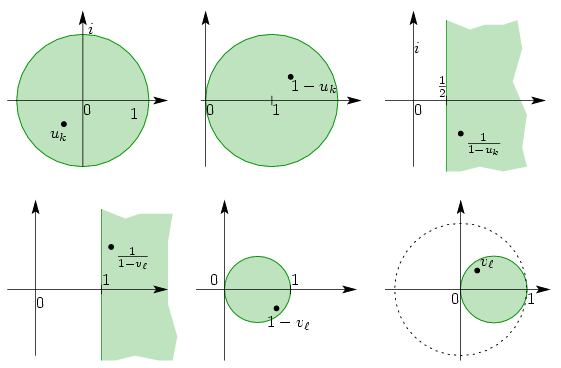
$\sum_{\ell=1}^{n-1} \frac1{1-v_\ell} = 2\sum_{k=2}^m \frac1{1-u_k}.$

For every k, the number u_k lies in the unit disc (or on its boundary), and 1-u_k lies in the circle with center 1 and unit radius (or on its boundary). The operation of taking reciprocals can be considered as the combination of an inversion from pole 0 and mirroring over the real axis. Hence $\frac1{1-u_k}$ lies in the half plane $\mathrm{Re~}z\ge\frac12$ , i.e. $\mathrm{Re}\frac1{1-u_k}\ge\frac12$ .

Summing up these inequalities,

$\max\limits_{1\le\ell\le n-1} \mathrm{Re}\frac1{1-v_\ell} \ge \frac1{n-1}\sum_{\ell=1}^{n-1} \mathrm{Re}\frac1{1-v_\ell} = \frac2{n-1}\sum_{k=2}^m \mathrm{Re}\frac1{1-u_k} \ge 1,$

so at least one $\frac1{1-v_\ell}$ lies in the half plane $\mathrm{Re~}z\ge1$ .

Repeating the same geometric steps backwards,

$\mathrm{Re}\frac1{1-v_\ell}\ge1 \iff \bigg|(1-v_\ell)-\frac12\bigg|\le\frac12 \iff \bigg|v_\ell-\frac12 \bigg|\le\frac12 \Longrightarrow \mathrm{Re}~v_\ell\ge0.$

Statistics:

3 students sent a solution.

5 points: Tomon István.

4 points: Nagy 235 János.

Unfair, not evaluated: 1 solutions.

Problems in Mathematics of KöMaL, May 2007

3 students sent a solution.
5 points:	Tomon István.
4 points:	Nagy 235 János.
Unfair, not evaluated:	1 solutions.

Already signed up?
New to KöMaL?