 Problem A. 433. (September 2007)
Problem A. 433. (September 2007)
A. 433. Prove that if a, b, c are real numbers such that a2+b2+c2=1 then .
(Proposed by János Bodnár, Budapest)
(5 pont)
Deadline expired on October 15, 2007.
Solution 1. Let ,
and
. For these variables the constraint can be re-written as
| (1-u)2+(1-v)2+(1-w)2=2(a2+b2+c2)=2; | (1a) |
| u2+v2+w2=2(u+v+w)-1; | (1b) |
| (1c) |
The statement to prove is
uvw uv+vw+wu.
uv+vw+wu.
Case 1: u,v,w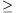 0. From the constraint
0. From the constraint , hence
; it can be obtained similarly that v<3 and w<3. Therefore
Case 2: at least one of u,v,w is negative. Equation (1a) cannot hold if two of them are negative; so exactly one of u,v,w is negative. Then
Solution 2. By the constraint we have 2ab a2+b2
a2+b2 a2+b2+c2=1 and similarly 2ac
a2+b2+c2=1 and similarly 2ac 1, 2bc
1, 2bc 1.
1.
Then
2-(a+b+c-2abc)2=1+(a2+b2+c2)-(a+b+c-2abc)2=(1-2ab)(1-2ac)(1-2bc)+4a2b2c2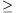 0
0
and therefore
From the solution of Tuan Nhat Le
Statistics:
16 students sent a solution. 5 points: Blázsik Zoltán, Huszár Kristóf, Korándi Dániel, Lovász László Miklós, Nagy 235 János, Nagy 314 Dániel, Szűcs Gergely, Tomon István, Tossenberger Anna, Tuan Nhat Le, Wolosz János. 1 point: 1 student. 0 point: 4 students.
Problems in Mathematics of KöMaL, September 2007
