Mathematical and Physical Journal
for High Schools
Issued by the MATFUND Foundation
Already signed up?
New to KöMaL?

Problem A. 522. (December 2010)

A. 522. The vertices and side arcs of the spherical hexagon ABCDEF are located on a hemisphere. The arc AB is perpendicular to the arc BC, the arc AF is perpendicular to the arc EF, moreover AB=AF, BC=CD and DE=EF. Prove that the great arcs AD and CE are perpendicular.

(5 pont)

Deadline expired on January 10, 2011.

Sorry, the solution is available only in Hungarian. Google translation

1. megoldás. Legyen a félgömb középpontja O. A D-ben fektetett érintősík messe az OC és OE egyeneseket OC-ben, illetve OE-ben. A OC és OE középpontú, D-n átmenő gömböket jelöljük {\cal G}_C-vel, illetve {\cal G}_C-vel. Ezek merőlegesen metszik a félkört, és -- mivel BC=CD és DE=EF -- illeszkednek B-re, illetve F-re.

Az AB ív a {\cal G}_C-hez B-ben fektetett érintősíkban van, ezért az AB szakasz érinti {\cal G}_C-t. Hasonlóképp, az AF szakasz érinti {\cal G}_E-t.

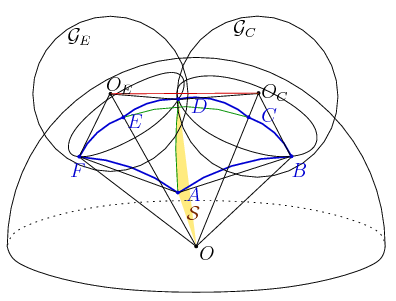
Jelöljük {\cal S}-sel a {\cal G}_C és {\cal G}_E gömbök hatványsíkját. A D pont közös pontja a gömböknek, tehát rajta van a hatványsíkon. Mivel AB=AF, az A pontból húzott AB és AF érintő szakaszok ugyanakkorák, tehát A is a hatványsíkon van. Mivel pedig a két gömb merőlegesen metszi a félgömböt, az O pont is az \mathcal{S} síkon van. (Az OD szakasz mindkét gömböt érinti.)

A két gömb centrálisa, az OCOE egyenes merőleges a hatványsíkra. Ebből következik, hogy a centrálisra illeszkedő OOCOE sík merőleges a hatványsíkra. Mivel mindkét sík tartalmazza a félgömb O középpontját, a félgömbből merőleges főköríveket metszenek ki: az OOCOE sík és a félgömb metszete a CE ív, az \mathcal{S} sík és a félgömb metszete pedig az AD ív meghosszabbítása.

 

2. megoldás (Frankl Nóra megoldása). Legyen a gömb középpontja O, a sugara egységnyi. Legyenek O-ból az A, B, C, D, E, F csúcsokba mutató vektorok rendre a, b, c, d, e, f. A csúcsok egy félgömbön helyezkednek el, azért a hatszög oldalait alkotó ívek egyike sem nagyobb \pi-nél. A gömbön két egyenes szöge a síkjaik szöge, egy XY ív hossza pedig a síkjában a hozzá tartozó középponti szög (XOY szög).

AB merőleges BC-re, ezért (a×b).(b×c)=0. (a×b az AOB sík normálvektora.) Ugyanígy (a×f).(e×f)=0.

A a.b szorzat az AB ívhez tartozó középponti szög koszinusza, tehát a.b=a.f. (Mert egy XY ív hosszát egyértelműen meghatározza az XOY középponti szög, tehát ennek koszinusza (Egy félgömbön helyezkednek el a pontok.).) Ugyanígy b.c=c.d és d.e=e.f.

A skaláris szorzás kommutatív és asszociatív és disztributív. Ha x, y, z és v négy vektor, akkor xyz=yzx=(x×y).z=x.(y×z). Ezt használva z×v-t egy vektornak tekintve: (x×y).(z×v)=x.(y×(z×v)), itt pedig a kifejtési tételt és disztributivitást használva: x.(y×(z×v))=x.((y.v).z-(y.z).v)=(y.v).(x.z)-(y.z).(x.v). Ezeket az azonosságokat fogjuk ezután többször használni.

(a×b).(b×c)=(b.c).(a.b)-(b2).(a.c)=0 és (a×f).(f×e)=(f.e).(a.f)-(f2).(a.e)=0, a bizonyítandó állítás pedig tulajdonképp az, hogy (a×d).(c×e)=(d.e).(a.c)-(d.c).(a.e)=L=0. Tehát azt kell igazolni, hogy L=0.

d.e=a.f és \bf{a}\cdot \bf{c}=\frac{(\bf{b}\cdot \bf{c})(\bf{a}\cdot \bf{f})}{\bf{b}^2} tehát (\bf{d}\cdot \bf{e})\cdot (\bf{a}\cdot \bf{c})=(\bf{a}\cdot \bf{f})\frac{(\bf{b}\cdot \bf{c})(\bf{a}\cdot \bf{f})}{\bf{b}^2}=\frac{(\bf{a}\cdot \bf{f})(\bf{b}\cdot \bf{c})(\bf{a}\cdot \bf{f})}{\bf{b}^2}. Hasonlóan átalakítható (d.c).(a.e) is. (\bf{d}\cdot \bf{c} )\cdot (\bf{a}\cdot \bf{e})=\frac{(\bf{a}\cdot \bf{f})(\bf{b}\cdot \bf{c})(\bf{a}\cdot \bf{f})}{\bf{f}^2}. De f2=b2=1, ezért L tényleg 0.

Statistics:

11 students sent a solution.
5 points:Ágoston Tamás, Backhausz Tibor, Damásdi Gábor, Frankl Nóra, Janzer Olivér, Mester Márton, Nagy 235 János, Nagy 648 Donát, Strenner Péter, Szabó 928 Attila.
0 point:1 student.

Problems in Mathematics of KöMaL, December 2010