 Problem A. 547. (November 2011)
Problem A. 547. (November 2011)
A. 547. A tetrahedron OA1A2A3 is given. For i=1,2,3 let Bi be a point in the interior of the edge OAi and let Ci be a point on the ray OAi, beyond Ai. Suppose that the polyhedron bounded by the six planes OAi+1Ai+2 and BiAi+1Ai+2 (i=1,2,3) circumscribes a sphere, and the polyhedron bounded by the planes BiAi+1Ai+2 and CiAi+1Ai+2 also circumscribes a sphere. Prove that the polyhedron bounded by the planes OAi+1Ai+2 and CiAi+1Ai+2 also circumscribes a sphere.
(5 pont)
Deadline expired on December 12, 2011.
Solution (outline). We will use oriented lines, planes and angles. For arbitrary, non-collinear points X,Y,Z, the orinetation of the line XY the same as the direction of the vector , and the vector
points into the positive side of the plane XYZ,
Lemma. Let  be an oriented line which is contained by the oriented planes
be an oriented line which is contained by the oriented planes ,
and
. Let
be the angle by which the plane
can be rotated to
around
 (i=1,2; these angles are considered modulo 360o). Suppose that some point X has signed distances d,r,-r from the planes
(i=1,2; these angles are considered modulo 360o). Suppose that some point X has signed distances d,r,-r from the planes ,
,
, respectively. Then we have
Proof. Denote by the unit normal vector of the plane
which points to the positive side of the plane and let
be the direction vector of the line
 Let
Let be a vector from a point of
 to X. Then
to X. Then
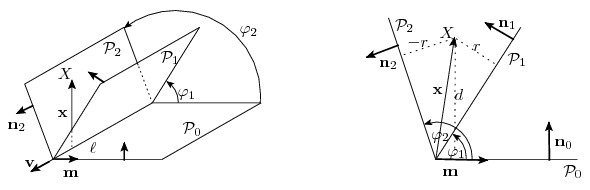
Let .Then
Taking the dot-product with ,
sin  2.r-sin
2.r-sin  1.(-r)=sin (
1.(-r)=sin ( 2-
2- 1).d
1).d
From this we get
The lemma is proved.
Let X and rX be the center and radius of the sphere, respectively, which is circumcribed by the planes OAi+1Ai+2 and BiAi+1Ai+2. Let dX be the signed distance between X and the plane A1A2A3 síktól dX. The signed distances between X and the planes BiAi+1Ai+2 are all rX, and the signed distances between X and the planes OAi+1Ai+2 are all -rX.
Analogously, let Y and rY be the center and radius of the sphere which is circumscribed by the planes BiAi+1Ai+2 and CiAi+1Ai+2. let dY by the signed distance between Y and the plane A1A2A3. The signed distances between Y and the planes CiAi+1Ai+2 are all rY, and the signed distances between X and the planes BiAi+1Ai+2 are all -rY.
For every i=1,2,3 take the external angle bisector of the planes Ai+1Ai+2O and Ai+1Ai+2Ci, and let Z be the intersection point of the three angle bisector planes --- Z will be center of the desired sphere. (Now assume that none of the angle bisectors coincides with the plane A1A2A3; then the point Z is unique and does not lie on A1A2A3.)
Let dZ and  be the signed distance between Z and A1A2A3 and A1A2C3, respectively. Since Z lies on the external angle bisector between A1A2C3 and A1A2O, the signed distance between Z and A1A2O is -
be the signed distance between Z and A1A2A3 and A1A2C3, respectively. Since Z lies on the external angle bisector between A1A2C3 and A1A2O, the signed distance between Z and A1A2O is - .
.
Let  =
= (A1A2A3,A1A2O),
(A1A2A3,A1A2O),  =
= (A1A2A3,A1A2B3) and
(A1A2A3,A1A2B3) and  =
= (A1A2A3,A1A2C3), where the angles are measured around the oriented line A1A2.
(A1A2A3,A1A2C3), where the angles are measured around the oriented line A1A2.
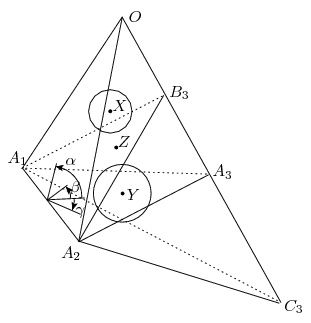
Applying the Lemma for the line A1A2, the planes A1A2A3, A1A2B3, A1A2O and the point X we get
| (1) |
Similarly, applying the Lemma for the line A1A2, the planes A1A2A3, A1A2C3, A1A2B3 and the point Y we get
| (2) |
Finally, Similarly, applying the Lemma for the line A1A2, the planes A1A2A3, A1A2C3, A1A2O and the point Y we obtain
As can be seen, due to dZ 0 the distances dX,rX,dY,rY,dZ determine
0 the distances dX,rX,dY,rY,dZ determine  . If we cyclicly shift the indices 1,2,3, we obtain the same value. Hence, the point Z has the same distance from all planes OAi+1Ai2 and CiAi+1Ai2.
. If we cyclicly shift the indices 1,2,3, we obtain the same value. Hence, the point Z has the same distance from all planes OAi+1Ai2 and CiAi+1Ai2.
In the particular case when some planes CiAi+1Ai+2 and OAi+1Ai+2 are symmetric over A1A2A3, the points C1,C2,C3 can be moved in such a way that the three spheres exist; then the original configuration can be considered as a limit case.
Statistics:
2 students sent a solution. 0 point: 2 students.
Problems in Mathematics of KöMaL, November 2011
