 Problem A. 550. (December 2011)
Problem A. 550. (December 2011)
A. 550. Is it true that every sufficiently large positive integer is the sum of a Fibonacci number and a prime number?
(5 pont)
Deadline expired on January 10, 2012.
Solution (outline). The answer is NO. There are infinitely many positive integers which cannot represented as the sum of a Fibonacci number and a prime number. To prove this, we cover the Fibonacci numbers with a finite number of arithmetic progressons whose differences are distinct primes.
It is well-known that if we consider the sequence of Fibonacci numbers modulo some positive integer m, then the sequence of remainders is periodic. Usually the period is denoted by 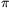 (m) and called as Pisano-period. (Fibonacci = Leonard Pisano.) For instance, in the case m=11 we have
(m) and called as Pisano-period. (Fibonacci = Leonard Pisano.) For instance, in the case m=11 we have 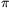 (11)=10, and the first period is (1,1,2,3,5,8,2,10,1,0). As can be seen, there can be equal elements in the same period; for example, for m>2, the remainder 1 appears at least three times since F-1=F1=F2=1.
(11)=10, and the first period is (1,1,2,3,5,8,2,10,1,0). As can be seen, there can be equal elements in the same period; for example, for m>2, the remainder 1 appears at least three times since F-1=F1=F2=1.
|
Table 1
In Table 2, for each prime p above we chose a residue class modulo p, listed in the second column. In the Fibonacci sequence these remainders appear among a few arithmetic progressions of the indices; these are shown in the first column. Every row can be interpreted as if n belongs to the residue class in the first entry of the row then Fn belongs to the residue class in the second entry.
|
Table 2
The most important property of this table is that the residue classes in the first column cover all integer numbers. Hence, the union of the residue classes in the second column cover all Fibonacci numbers.
After finding Table 2, we can solve the problem. Let M=2.3.5.11.19.31.41.61.107.181.541. By the Chinese Remainder Theorem there is poisitive integer A such that ,
,
,
,
and
. Then, for all pairs k,n of positive integers, Mk+A-Fn is divisible by either 2, 3, 5, 11, 19, 31, 41, 61, 107, 181 or 541.
The sequence of the numbers of the form Fn+2, Fn+3, ..., Fn+541 has zero density, while the arithmetic progression Mk+A has positive density. Therefore, the numbers which cannot be represented as the sum of a Fibonacci number and a prime has positive (lower) density.
Statistics:
6 students sent a solution. 5 points: Ágoston Tamás, Mester Márton. 2 points: 2 students. 0 point: 2 students.
Problems in Mathematics of KöMaL, December 2011
