Problem A. 560. (April 2012)

A. 560. Given a right circular cone with vertex O, and a fixed point P in the base plane of the cone. Draw a line x through P which intersects the base circle of the cone at two points, X₁ and X₂. Show that $\tan\frac{\angle POX_1}2 \cdot \tan\frac{\angle POX_2}2$ does not depend on the choice of the line x.

(5 pont)

Deadline expired on May 10, 2012.

Solution. Let G be the sphere with center O that contains the base circle of the cone. Let P' be the intersection of G with the ray OP, and let I be the point of G, diametrically opposite with P'.

Apply inversion to the sphere with center I and radius IP'. The image of G is the tangent plane S at point P'. The image of the base circle is some circle k in the plane S.

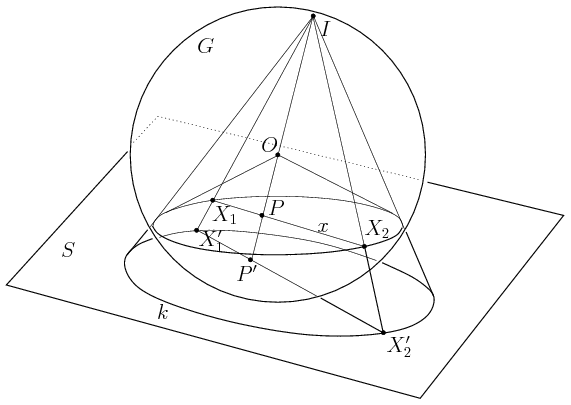
Let X₁' and X₂' be the images of X₁ and X₂, respectively. The points P',X₁',X₂' are collinear, moreover X₁',X₂' lie on k. Then

$\tg \frac{POX_1\sphericalangle}2 \cdot \tg \frac{POX_2\sphericalangle}2 = \tg P'IX_2' \sphericalangle \cdot \tg P'IX_2' \sphericalangle = \frac{P'X_1'}{IP'} \cdot \frac{P'X_2'}{IP'} = \frac{P'X_1' \cdot P'X_2'}{IP'^2}.$

The numerator, being the power of P' with respect to k, does not depend on the points X₁',X₂'.

Statistics:

8 students sent a solution.

5 points: Ágoston Tamás, Janzer Olivér, Mester Márton, Omer Cerrahoglu, Strenner Péter, Szabó 789 Barnabás, Szabó 928 Attila.

4 points: Gyarmati Máté.

Problems in Mathematics of KöMaL, April 2012

8 students sent a solution.
5 points:	Ágoston Tamás, Janzer Olivér, Mester Márton, Omer Cerrahoglu, Strenner Péter, Szabó 789 Barnabás, Szabó 928 Attila.
4 points:	Gyarmati Máté.

Already signed up?
New to KöMaL?