Problem A. 568. (September 2012)

A. 568. Given a triangle ABC and a line $\ell$ through its incenter. Denote by A', B' and C' the mirror images of A, B and C about $\ell$ , respectively. Let the lines through A', B' and C', parallel to $\ell$ , meet the lines BC, CA and AB at P, Q and R, respectively. Prove that the points P, Q and R lie on a line and this line is tangent to the incircle.

(5 pont)

Deadline expired on October 10, 2012.

Sorry, the solution is available only in Hungarian. Google translation

Megoldásvázlat. Mivel az $\ell$ egyenes átmegy a beírt kör középpontján, az A'B', B'C', C'A' egyenesek is érintik a beírt kört. Rajzoljuk meg a P ponton át a beírt kör másik, B'C'-től különböző érintőjét is; messe ez az érintő a CA és AB egyeneseket a Q^*, illetve az R^* pontban. Azt akarjuk megmutatni, hogy Q^*=Q és R^*=R.

Legyen I az $\ell$ egyenes ideális pontja. Legyen U az $\ell$ , a BC és a B'C' egyenesek közös pontja, V az $\ell$ , a CA és a C'A' egyenesek közös pontja, és W az $\ell$ , a AB és a A'B' egyenesek közös pontja. (Mivel az A',B',C' pontok az A,B,C pontok $\ell$ -re vontakozó tükörképei, ezek a pontok valóban léteznek.)

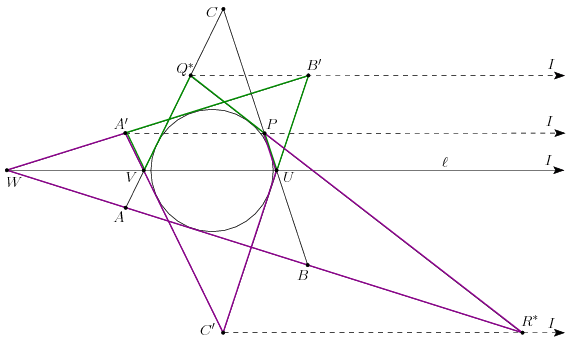
Alkalmazzuk a Brianchon-tételt a A'VQ^*PUB' hurkolt hatszögre, amelynek oldalegyenesei érintik a beírt kört. A tétel szerint a hatszög A'P, VU és Q^*B' átlóegyenesei egy ponton mennek át. Mivel A'P és VU= $\ell$ párhuzamos, a közös pont I, vagyis Q^*B' is párhuzmos $\ell$ -el. Ugyanakkor a az A'C' egyenesnek Q az a pontja, amire QB' párhuzmos $\ell$ -el. Tehát Q^*=Q.

Hasonlóan, a Brianchon-tételt az A'WR^*PUC' érintőhatszögre alkalmazva láthatjuk, hogy R^*C' is prhuzamos $\ell$ -el, következésképpen R^*=R.

Megjegyzés. Vannak olyan elfajuló esetek, amikor a megoldás nem mondható el ebben a formában; például ha valamelyik csúcs az $\ell$ egyenesre esik, vagy valamelyik oldal merőleges $\ell$ -re. Az ilyen eseteket külön meg kell vizsgálnunk, vagy pedig az általános eset határeseteiként kell előállítanunk.

Statistics:

7 students sent a solution.

5 points: Herczeg József, Ioan Laurentiu Ploscaru, Janzer Olivér, Nagy Róbert, Szabó 928 Attila.

2 points: 2 students.

Problems in Mathematics of KöMaL, September 2012

7 students sent a solution.
5 points:	Herczeg József, Ioan Laurentiu Ploscaru, Janzer Olivér, Nagy Róbert, Szabó 928 Attila.
2 points:	2 students.

Already signed up?
New to KöMaL?