 Problem A. 569. (October 2012)
Problem A. 569. (October 2012)
A. 569. Call a set interesting if 2y-x
 A for all pairs x,y
A for all pairs x,y A with x<y. Let a1<a2<...<ak be positive integers (k
A with x<y. Let a1<a2<...<ak be positive integers (k 2) whose greatest common divisor is 1. Prove that if A is an interesting set and
2) whose greatest common divisor is 1. Prove that if A is an interesting set and then a1+ak-3
 A.
A.
Proposed by: Carlos Gustavo T. A. Moreira (Gugu), Rio de Janeiro
(5 pont)
Deadline expired on November 12, 2012.
Solution. We prove a more general statement.
Lemma. If a0<a1<...<ak (k 2) are elements of an interesting set A, the greatest common divisor of (a1-a0), (a2-a0), ..., (ak-a0) is 1, and s=ak+a1-a0-3, then {s,s+1,s+2,...}
2) are elements of an interesting set A, the greatest common divisor of (a1-a0), (a2-a0), ..., (ak-a0) is 1, and s=ak+a1-a0-3, then {s,s+1,s+2,...}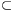 A.
A.
In the particular case a0=0 this implies s A.
A.
We prove the Lemma by induction on (ak-a0).
In the case ak-a0 2 we have k=2, a1=a0+1 and a2=a0+2, therefore s=a2+a1-a0-3=a0. So, s=a0
2 we have k=2, a1=a0+1 and a2=a0+2, therefore s=a2+a1-a0-3=a0. So, s=a0 A, s+1=a1
A, s+1=a1 A, és s+2=a2
A, és s+2=a2 A. The set A is interesting, for every integer x, x
A. The set A is interesting, for every integer x, x A and x+1
A and x+1 A impiles x+2=2(x+1)-x
A impiles x+2=2(x+1)-x A. Hence, s,s+1,s+2,... are all elements of A.
A. Hence, s,s+1,s+2,... are all elements of A.
Now suppose that ak-a0>2, and consider the numbers a1,a2,...,ak and 2a1-a0. We will apply the induction hypothesis to these numbers.
Since A is interesting 2a1-a0 A. Among 2a1-a0,a1,a2,...,ak the number a1 is the smallest. The greatest common divisor of (a2-a1),...,(ak-a1) and (2a1-a0)-a1) also is 1, due to (ai-a1,(2a1-a0)-a1)=(ai-a1,a1-a0)=(ai-a0,a1-a0).
A. Among 2a1-a0,a1,a2,...,ak the number a1 is the smallest. The greatest common divisor of (a2-a1),...,(ak-a1) and (2a1-a0)-a1) also is 1, due to (ai-a1,(2a1-a0)-a1)=(ai-a1,a1-a0)=(ai-a0,a1-a0).
Case 1: There are at most 2 different values among 2a1-a0,a1,a2,...,ak.
Since a2,...,ak and 2a1-a0 are all greater thatn a1, this means k=2 and 2a1-a0=a2. Then a2-a0=2(a1-a0). The numbers a2-a0 and a1-a0 must be co-primes, so a1-a0=1 and a2-a0=2; this contradicts the assumption ak-a0>2.
Case 2: There are at least 3 distict values among 2a1-a0,a1,a2,...,ak, and 2a1-a0<a2.
Apply the induction hypothesis to b0=a1<b1=2a1-a0<b2=a2<...<bk=ak. (This is allowed by bk-b0=ak-a1<ak-a0.) Let t=bk+b1-b0-3. By the hypothesis . Due to t=ak+(2a1-a0)-a1-3=s, this is what we need.
Case 3: There are at least 3 distict values among 2a1-a0,a1,a2,...,ak, and 2a1-a0>ak.
Apply the induction hypothesis to b0=a1,b1=a2,...,bk-1=ak,bk=2a1-a0. (Not that bk-b0=a1-a0<ak-a0.) Let t=bk+b1-b0-3. By the hypothesis, {t,t+1...}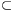 A. By t=(2a1-a0)+a2-a1-3=a2+a1-a0-3
A. By t=(2a1-a0)+a2-a1-3=a2+a1-a0-3 s, we have {s,s+1,...}
s, we have {s,s+1,...}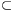 {t,t+1,...}
{t,t+1,...}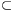 A.
A.
Case 4: There are at least 3 distict values among 2a1-a0,a1,a2,...,ak, and a2 2a1-a0
2a1-a0 ak.
ak.
Sort the numbers a1,...,ak and 2a1-a0 in increasing order; let the ordered sequence be , where
 =k or
=k or  =k-1, b0=a1, b1=a2 és
=k-1, b0=a1, b1=a2 és .
Let . Due to b
 -b0=ak-a1<ak-a0, we can apply the induction hypothesis to get {t,t+1,...}
-b0=ak-a1<ak-a0, we can apply the induction hypothesis to get {t,t+1,...}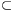 A. Since t=ak+a2-a1-3
A. Since t=ak+a2-a1-3 ak+(2a1-a0)-a1-3=s, we have {s,s+1,...}
ak+(2a1-a0)-a1-3=s, we have {s,s+1,...}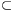 {t,t+1,...}
{t,t+1,...}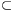 A.
A.
Statistics:
8 students sent a solution. 5 points: Janzer Olivér, Nagy Róbert, Omer Cerrahoglu, Szabó 789 Barnabás. 1 point: 1 student. 0 point: 3 students.
Problems in Mathematics of KöMaL, October 2012
