Problem A. 573. (November 2012)

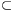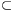A. 573. Let D={0,1,2,...,9} be the set of decimal digits, and let R $\subset$ D×D be a set of ordered pairs of digits. An infinite sequence (a₁,a₂,a₃,...) of digits is said to be compatible with R if (a_j,a_j+1) $\in$ R for all positive integer j. Determine the smallest positive integer K with the property that if an arbitrary set R $\subset$ D×D is compatible with at least K distinct digit sequences then R is compatible with infinitely many digit sequences.

Based on the 5th problem of CIIM 2012, Guanajuato, Mexico

(5 pont)

Deadline expired on December 10, 2012.

Statistics:

15 students sent a solution.

5 points: Ágoston Péter, Fehér Zsombor, Janzer Olivér, Maga Balázs, Omer Cerrahoglu, Vályi András, Williams Kada, Zilahi Tamás.

4 points: Herczeg József, Ioan Laurentiu Ploscaru.

2 points: 2 students.

1 point: 1 student.

0 point: 2 students.

Problems in Mathematics of KöMaL, November 2012

15 students sent a solution.
5 points:	Ágoston Péter, Fehér Zsombor, Janzer Olivér, Maga Balázs, Omer Cerrahoglu, Vályi András, Williams Kada, Zilahi Tamás.
4 points:	Herczeg József, Ioan Laurentiu Ploscaru.
2 points:	2 students.
1 point:	1 student.
0 point:	2 students.

Already signed up?
New to KöMaL?