 Problem A. 574. (November 2012)
Problem A. 574. (November 2012)
A. 574. Let n 2 and let
2 and let be a polynomial with real coefficients. Prove that if for some positive integer k the polynomial (x-1)k+1 divides p(x) then
.
CIIM 2012, Guanajuato, Mexico
(5 pont)
Deadline expired on December 10, 2012.
Solution. For convenience, define the leading coefficient an=1 also.
Lemma. For every polynomial q(y) with degree at most k, we have .
Proof. Let  0(y)=1 and let
0(y)=1 and let for
. By (x-1)k|p(x), for 0

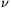
 k we have
k we have
Every polynomial with degree at most k can be repesented as a linear combination of the polynomials , so
with some real numbers
. Then
To prove the problem statement, let Tk be the kth Chebyshev-polynomial, and choose
Then , and
(In the last step we applied the inequality .)
By applying the lemma,
Statistics:
3 students sent a solution. 5 points: Ioan Laurentiu Ploscaru. 1 point: 2 students.
Problems in Mathematics of KöMaL, November 2012
