 Problem A. 575. (December 2012)
Problem A. 575. (December 2012)
A. 575. Prove that if and
, then it is possible to select at most four, not necessarily distinct elements from S, whose sum is a power of 2.
Proposed by: Sándor Kiss, Budapest
(5 pont)
Deadline expired on January 10, 2013.
Solution. The origin of the problem is the book Additive Number Theory: Inverse Problems and the Geometry of Sumsets by Melvyn B. Nathanson (pages 31-33.).
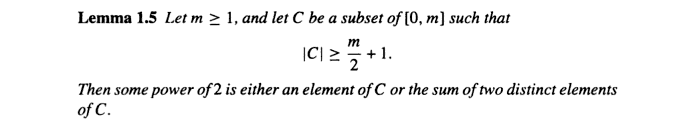


Statistics:
1 student sent a solution. 0 point: 1 student.
Problems in Mathematics of KöMaL, December 2012
