Problem A. 597. (October 2013)

A. 597. The circles k₀, k₁, k₂, k₃ and k₄ lie in the plane in such a way that for i=1,2,3,4 the circle k_i is externally tangent to k₀ at point T_i, and k_i is externally tangent to k_i+1 at point S_i (k₅=k₁). Let O be the center of k₀. Let the lines T₁T₃ and T₂T₄ meet at T, and let the lines S₁S₃ and S₂S₄ meet at S. Prove that the points O, T and S are collinear.

Proposed by: Márton Mester, Cambridge

(5 pont)

Deadline expired on November 11, 2013.

Sorry, the solution is available only in Hungarian. Google translation

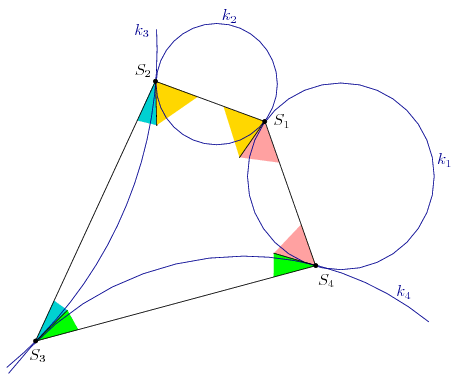
1. megoldás (vázlat). Először megmutatjuk, hogy az S₁, S₂, S₃, S₄ pontok egy körön vannak. Jelöljük t_i-vel a k₁ és k_i+1 közös belső érintőjét. Az S_iS_i+1 húrok ugyanakkora szöget zárnak be a t_i és t_i-1 érintőkkel. Ebből láthatjuk, hogy az S₁S₂S₃S₄ négyszög szemközti összeinek összege egyenlő, S₁S₂S₃S₄ húrnégyszög. Jelöljük a körülírt körét u-val, u középpontját U-val.

Legyen x és y az a két kör, ami átmegy T₁-en és T₃-on, illetve T₂-n és T₄-en, továbbá merőleges k₀-ra. A k₁ és k₃ szintén merőleges x-re, az x-re való tükrözés (inverzió) ezért önmagára képezi a k₀, k₁ és k₃ köröket. Mivel k₀, k₁ és k₃ egyértelműen meghatározza k₂-t és k₄-et, a k₂ és k₄ egymás x-re vonatkozó tükörképe. Ebből következik, hogy a T₂ és T₄ pontok, az S₁ és S₄ pontok, továbbá az S₂ és S₃ pontok is egymás x-re vonatkozó tükörképei, az y kör pedig önmaga tükörképe, tehát x és y merőleges egymásra. Az u kör szintén önmaga tükörképe, ezért u is merőleges x-re. Hasonlóan, a k₁ és k₃ körök, a T₁ és T₃ pontok, az S₁ és S₂ pontok, illetve a S₃ és S₄ pontok egymás y-ra vonatkozó tükörképei, továbbá az y kör merőleges k₀-ra, k₂-re, k₄-re és u-ra.

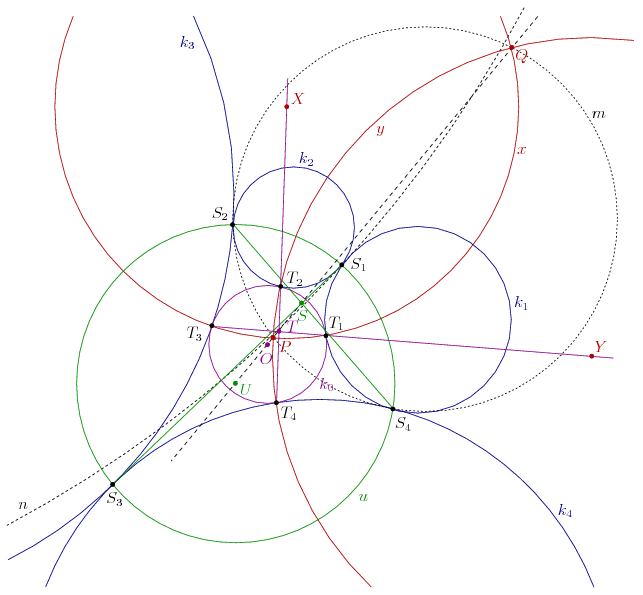
Legyen P és Q az x és y körök két metszéspontja. Azt fogjuk megmutatni, hogy O, U, T és S is az x és y körök PQ hatványvonalán van.

Mivel x és y is merőleges k₀-ra, a P és Q pontok egymás tükörképei a k₀ körre, ezért k₀ középpontja, O is a PQ egyenesen van. Hasonlóan, mivel u merőleges x-re és y-ra, az u középpontja, U is a hatványvonalon van.

Az T₁T₃ egyenes a k₀ és az x hatványvonala, az T₂T₄ egyenes pedig a k₀ és az y hatványvonala. Tehát T a k₀, x és y körök hatványpontja. ami a harmadik hatványvonalon, az PQ egyenesen van.

Tekintsük most a PQS₁, PQS₂ és PQS₄, köröket. A PQS₁ tükörképe x-re PQS₄, y-ra PQS₂. Mivel x és y merőleges egymásra, a PQS₄ és PQS₂ iránya a P és Q pontban megegyezik. Tehát a PQS₄ és a PQS₂ kör ugyanaz; jelöljük ezt a kört m-mel. Hasonlóan látjuk, hogy P,Q,S₁,S₃ egy körön van; ezt a kört jelöljük n-nel. Az u, m és n körök hatványpontja az S=S₁S₃S₂S₄ pont, amin átmegy m és n hatványvonala, a PQ egyenes.

Ezzel bebizonyítottuk, hogy az O, S és T pontok a PQ egyenesen vannak.

A megoldás akkor is elmondható, ha az x és y körök valamelyike egyenessé fajul. Ha mindkettő egyenes, akkor az O,U,S,T pontok egybeesnek.

2. megoldás (vázlat). Az előző megoldáshoz hasonlóan láttjuk, hogy S₁S₂S₃S₄ húrnégyszög, körülírt köre legyen u, középpontja U. Az u kör S_iS_i+1 íve a k_i+1 körben fekszik, így a k₁,k₂,k₃,k₄ körök lefedik u-t, míg ugyezek a körök kívülről érintik k₀-t. Ezért a k₀ és u közöknek ninics közös pontja. Ebből következik, hogy létezik olyan térbeli inverzió, ami a k₀ és u köröket párhuzamos (síkú) körökbe viszi. Tekintsünk egy ilyen inverziót; a pólusa legyen X, az egyes objektumok képét ' fogja jelölni a szokásos módon. A sík képe egy gömbfelület, a körök és egyenesek képe egy-egy, a gömbre illeszkedő kör; egymást érintő görbék képei egymást érintő görbék.

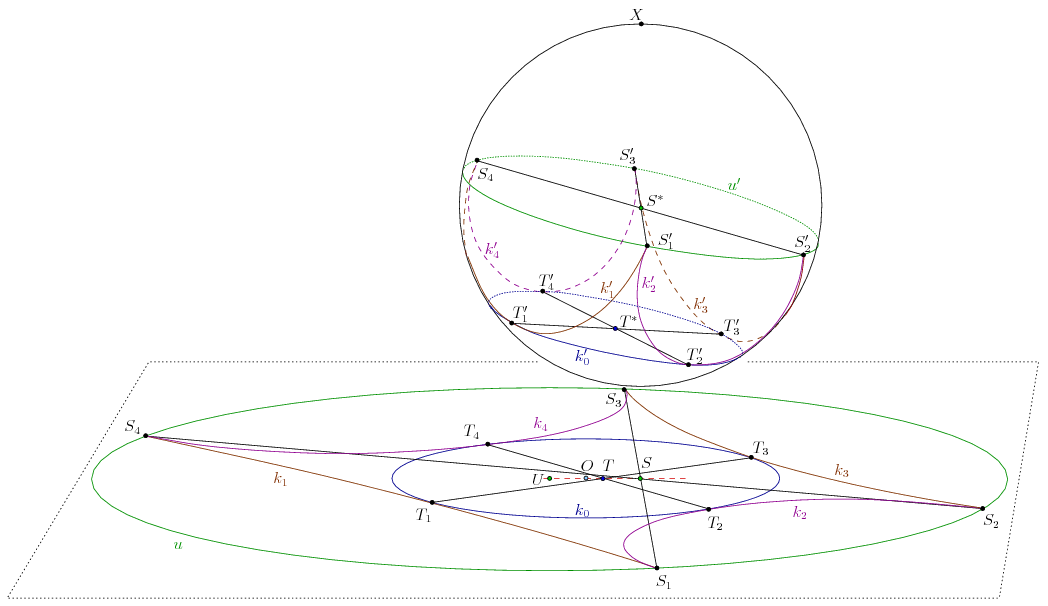
Minden egyes i-re a k_i' és u' körök szöge, valamint a k_i+1' és u' körök szöge 180^o-ra egésziti ki egymást. Ebből következik, hogy k₁' és k₃', illetve k₂' és k₄' ugyanakkora, S₁'S₂'S₃'S₄' téglalap, T₁'T₂'T₃'T₄' pedig négyzet.

Legyen S^*=S₁'S₃'S₃'S₄' és T^*=T₁'T₃'T₃'T₄' az u', iletve a k₀' kör középpontja. Mivel X, T_i és T_i' egy egyenesre esik, az X,T_i,T_i+2,T_i',T_i+2' pontok egy síkra esnek (i=1,2). E két sík metszésvonala XT^*T. Hasonlóan, X,S^*,S egy egyenesen van.

Az XS^*T^* síkra a k₀' és az u' kör is szimmetrikus, ezért az inverzeik is; ezért középpontjaik, O, illetve U a XS^*T^* síkban van.

Az O,U,S,T pontok mindegyike az eredeti sík és a XS^*T^* sík közös részén helyezkedik el, ez a négy pont tehát egy egyenesen van.

Megjegyzés. Térbe kilépés helyett az k₀ és u köröket koncentrikus körökbe is átvihetjük alkalmas inverzióval. Az Olvasóra bízzuk ennek a megközelítésnek a befejezését.

Statistics:

9 students sent a solution.
5 points:	Fehér Zsombor, Machó Bónis, Maga Balázs, Simon 047 Péter, Szabó 789 Barnabás, Williams Kada.
2 points:	1 student.
0 point:	2 students.

Problems in Mathematics of KöMaL, October 2013