 Problem A. 613. (March 2014)
Problem A. 613. (March 2014)
A. 613. There is given a convex quadrilateral \(\displaystyle ABCD\). The points \(\displaystyle E\) and \(\displaystyle F\) lie on the line segment \(\displaystyle AB\), \(\displaystyle G\) and \(\displaystyle H\) lie on \(\displaystyle BC\), \(\displaystyle I\) and \(\displaystyle J\) lie on \(\displaystyle CD\), and \(\displaystyle K\) and \(\displaystyle L\) lie on \(\displaystyle DA\) in such a way that \(\displaystyle AE<AF<AB\), \(\displaystyle BG<BH<BC\), \(\displaystyle CI<CJ<CD\), and \(\displaystyle DK<DL<DA\). The line \(\displaystyle EJ\) meets \(\displaystyle GL\) and \(\displaystyle HK\) at \(\displaystyle P\) and \(\displaystyle S\), and \(\displaystyle FI\) meets \(\displaystyle GL\) and \(\displaystyle HK\) at \(\displaystyle Q\) and \(\displaystyle R\), respectively. The points \(\displaystyle P\) and \(\displaystyle R\) lie on the diagonal \(\displaystyle AC\) and the points \(\displaystyle Q\) and \(\displaystyle S\) lie on \(\displaystyle BD\) (see the first cover). Suppose that each of the quadrilaterals \(\displaystyle AEPL\), \(\displaystyle BGQF\) and \(\displaystyle CIRH\) has an inscribed circle.
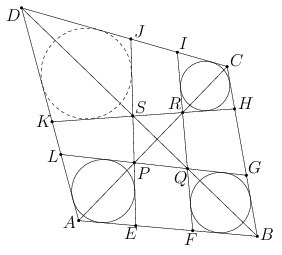
Show that the quadrilateral \(\displaystyle DKSJ\) also has an inscribed circle.
Based on a problem of the International Zhautykov Olympiad
(5 pont)
Deadline expired on April 10, 2014.
Statistics:
1 student sent a solution. 4 points: Fehér Zsombor.
Problems in Mathematics of KöMaL, March 2014
