 Problem A. 676. (September 2016)
Problem A. 676. (September 2016)
A. 676. Let \(\displaystyle \mathcal{K}\) be a circle with diameter \(\displaystyle OI\). Construct a one-to-one correspondence \(\displaystyle f \colon \mathcal{K}\setminus \{O,I\}\to\mathbb{R}\setminus\{0\}\) with the following property: for every four distinct points \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\) of \(\displaystyle \mathcal{K}\), other than \(\displaystyle O\) and \(\displaystyle I\), \(\displaystyle f(A)f(B)=f(C)f(D)\) is satisfied if and only if the lines \(\displaystyle AB\), \(\displaystyle CD\) and \(\displaystyle OI\) are concurrent or parallel to each other.
(5 pont)
Deadline expired on October 10, 2016.
Sorry, the solution is available only in Hungarian. Google translation
Megoldásvázlat. Egy lehetséges függvény \(\displaystyle f(X)= \pm\frac{IX}{XO} = \tg IOX\angle\), ahol az \(\displaystyle IOX\angle\) szöget előjelesen értjük: az értéke pozitív, ha az \(\displaystyle OIX\) háromszög pozitív körüljárású, illetve negatív, ha a háromszög negatív körüljárású. Az \(\displaystyle IOX\angle\) szög a \(\displaystyle 0\) kivételével minden értéket felvesz a \(\displaystyle (-\tfrac\pi2;\tfrac\pi2)\) intervallumban, így az \(\displaystyle f\) függvény is pontosan egyszer vesz fel minden \(\displaystyle 0\)-tól különböző valós értéket, vagyis \(\displaystyle f\) valóban egy kölcsönösen egyértelmű \(\displaystyle f \colon \mathcal{K}\setminus \{O,I\}\to\mathbb{R}\setminus\{0\}\) megfeleltetés.
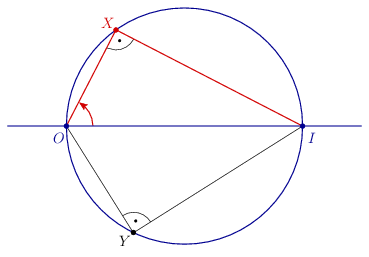
Az \(\displaystyle f\) függvény definíciójából láthatjuk, hogy tetszőleges \(\displaystyle X,Y\) pontokra
\(\displaystyle \frac{f(X)}{f(Y)} = \pm\frac{IX}{XO}:\frac{IY}{YO} = (I,O,X,Y), \)
ahol \(\displaystyle (I,O,X,Y)\) a négy pontnak a \(\displaystyle k\) körön vett kettősviszonya.
A feladatban előírt tulajdonság bizonyításához tekintsünk a körön négy tetszőleges, \(\displaystyle O\)-tól és \(\displaystyle I\)-től különböző pontot: \(\displaystyle A,B,C,D\)-t. Legyen az \(\displaystyle AB\) és \(\displaystyle OI\) egyenesek metszéspontja \(\displaystyle M\). (Ha \(\displaystyle AB\) és \(\displaystyle OI\) párhuzamos, akkor legyen \(\displaystyle M\) az \(\displaystyle OI\) egyenes ideális pontja.) A \(\displaystyle CM\) egyenes és a \(\displaystyle \mathcal{K}\) kör második, \(\displaystyle C\)-től különböző metszéspontja legyen \(\displaystyle D_1\). (Ha \(\displaystyle CM\) érinti a kört, akkor \(\displaystyle D_1=C\).)
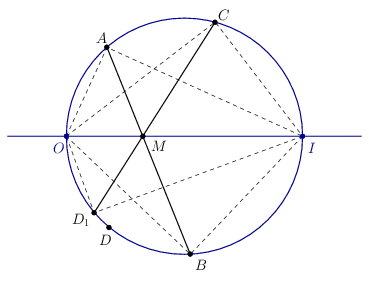
Az \(\displaystyle I,O,A,C\) pontokat az \(\displaystyle M\) ponton keresztül visszavetítve a körre, rendre az \(\displaystyle O,I,B,D_1\) pontokat kapjuk. Mint inverzió segítségével igazolható, egy körről (és így kúpszeletről) tetszőleges pontból önmagára visszavetítve, a pontnégyesek kettősviszonya megmarad. Ezért
\(\displaystyle \frac{f(A)}{f(C)} = (I,O,A,C) = (O,I,B,D_1) = (I,O,D_1,B) = \frac{f(D_1)}{f(B)}, \)
\(\displaystyle f(A) \cdot f(B) = f(C) \cdot f(D_1). \)
A \(\displaystyle CD\) egyenes akkor és csak akkor megy át az \(\displaystyle M\) ponton, ha \(\displaystyle D=D_1\), azaz, ha \(\displaystyle f(C)\cdot f(D) = f(C)\cdot f(D_1) = f(A)\cdot f(B)\).
Megjegyzés. Kettősviszonyok használata nélkül, például az \(\displaystyle MIA\) és \(\displaystyle MBO\), az \(\displaystyle MIB\) és \(\displaystyle MAO\), az \(\displaystyle MIC\) és \(\displaystyle MD_1O\), illetve az \(\displaystyle MID_1\) és \(\displaystyle MAC\) háromszögek hasonlóságából is levezethető, hogy
\(\displaystyle f(A) \cdot f(B) = f(C) \cdot f(D_1) = \frac{MI}{MO}. \)
(Az utolsó tört előjele negatív, ha az \(\displaystyle MI\) és \(\displaystyle MO\) szakaszok ellentétes irányúak.)
Statistics:
15 students sent a solution. 5 points: Baran Zsuzsanna, Borbényi Márton, Gáspár Attila, Imolay András, Lajkó Kálmán, Németh 123 Balázs, Tóth Viktor, Váli Benedek, Williams Kada. 4 points: Bukva Balázs, Cseh Kristóf, Egri Máté, Kerekes Anna, Matolcsi Dávid. 0 point: 1 student.
Problems in Mathematics of KöMaL, September 2016
