 |
Az A. 707. feladat (2017. november) |
A. 707. \(\displaystyle 100\) betyár áll a hortobágyi síkságon. Mindegyik illető egy \(\displaystyle 100^\circ\)-os szögtartományt lát. Az összes betyár felírja egy-egy papírra, hogy hány másik betyárt lát, majd mi összeadjuk ezt a \(\displaystyle 100\) számot. Mi a lehető legnagyobb összeg, amit ily módon kaphatunk?
(5 pont)
A beküldési határidő 2017. december 11-én LEJÁRT.
Válasz. Az összeg maximuma \(\displaystyle 8700\).
Megoldás. Vizsgáljuk azt a \(\displaystyle G\) irányított gráfot, melynek \(\displaystyle v_1,v_2,\dots,v_{100}\) csúcsai a betyárok, és melyben \(\displaystyle (v_i,v_j)\) irányított él pontosan akkor szerepel, ha az \(\displaystyle i\)-edik betyár látja a \(\displaystyle j\)-edik betyárt. Célunk maximalizálni \(\displaystyle G\) irányított éleinek számát.
Konstrukció. Helyezzük el a betyárokat a \(\displaystyle \{-1;1\}^2\) négyzet csúcsaihoz közel, egymás mögött. Vagyis, alkalmas \(\displaystyle \varepsilon>0\) mellett kerüljenek \(\displaystyle k=1,2,\dots,25\)-re a betyárok a
\(\displaystyle (\pm(1-k\varepsilon),\pm(1-k\varepsilon))\)
pontokba úgy, hogy a négyzet egy csúcsához közeli betyárnak a másik három csúcs látóterében legyen. (A \(\displaystyle PQR\angle \le 100^\circ\) feltétel a \(\displaystyle \overrightarrow{QP}\cdot \overrightarrow{QR}\ge |QP|\cdot |QR|\cdot \cos100^\circ\) feltétellel ekvivalens; ezzel ellenőrizhető, hogy ez valóban elérhető kellően kis \(\displaystyle \varepsilon>0\)-ra.)
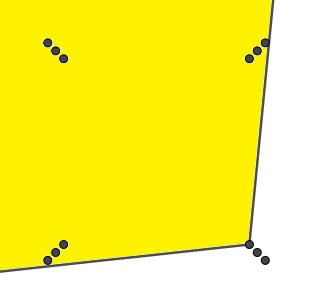
Ekkor \(\displaystyle G\) éleinek száma \(\displaystyle 2\cdot \binom{100}{2}-4\cdot \binom{25}{2}=8700\).
Bizonyítási ötlet. Hogy jobban fel tudjuk használni \(\displaystyle G\) éleinek korlátozásához azt a (gyenge) feltételt, hogy minden betyár csak \(\displaystyle 100^\circ\)-os szögben láthat, belátunk ebből egy olyan alakú feltételt, hogy "\(\displaystyle G\)-ben ... alakú részgráf nem szerepelhet". Ezt követően egy ügyes technikával becslést hozunk ki e feltételből.
Bizonyítás. Nem lehetséges, hogy \(\displaystyle 5\) betyár páronként lássa egymást. Tekintsük ugyanis az \(\displaystyle 5\) betyár konvex burkát. Mivel minden betyár \(\displaystyle 100^\circ\)-os látóterébe kell essen az összes betyár s így a konvex burok is, ezért minden betyár a konvex burok egy csúcsában helyezkedik el. Azonban egy konvex ötszög belső szögeinek átlaga \(\displaystyle 108^\circ\), így valamely szöge \(\displaystyle \ge 108^\circ\), ami ellentmond annak, hogy az annál a szögnél lévő betyár látja két szomszédját.
Tehát ha \(\displaystyle H\) az az egyszerű gráf, melynek csúcsai a betyárok, és melyben két betyárt éppen akkor kötünk össze, ha látják egymást, akkor \(\displaystyle H\)-ban nem lehet teljes \(\displaystyle 5\) csúcsú részgráf. Becslési eszközünk a Turán-tétel lesz, mely szerint ha egy \(\displaystyle 100\) csúcsú egyszerű gráfban nincs teljes \(\displaystyle 5\) csúcsú részgráf, akkor legfeljebb \(\displaystyle \binom{100}{2}-4\cdot \binom{25}{2}\) éle lehet. A Turán-tételt \(\displaystyle H\)-ra alkalmazva kapjuk, hogy \(\displaystyle G\) élszáma valóban legfeljebb
\(\displaystyle \binom{100}{2}+\left[\binom{100}{2}-4\cdot \binom{25}{2}\right]=8700.\)
Statisztika:
25 dolgozat érkezett. 5 pontot kapott: Bukva Balázs, Füredi Erik Benjámin, Gáspár Attila, Győrffy Ágoston, Imolay András, Matolcsi Dávid, Németh 123 Balázs, Saár Patrik, Schweitzer Ádám, Szabó Kristóf. 4 pontot kapott: Beke Csongor. 2 pontot kapott: 5 versenyző. 1 pontot kapott: 6 versenyző. 0 pontot kapott: 3 versenyző.
A KöMaL 2017. novemberi matematika feladatai

