 Problem A. 710. (December 2017)
Problem A. 710. (December 2017)
A. 710. For which \(\displaystyle n\) can we partition a regular \(\displaystyle n\)-gon into finitely many triangles such that no two triangles share a side?
(Based on a problem of the 2017 Miklós Schweitzer competition)
(5 pont)
Deadline expired on January 10, 2018.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Az elrendezést makroszinten vizsgáljuk: a feltételeket az elrendezést jellemző kombinatorikus mennyiségek bizonyos tulajdonságaivá alakítjuk át.
Ha \(\displaystyle n=3\), létezik megfelelő konstrukció, akár több háromszögre is:
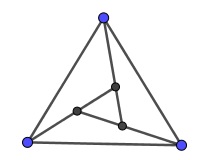
1. ábra
Belátjuk, hogy \(\displaystyle n\ge 4\) esetén azonban a kívánt konstrukció lehetetlen. Ehhez vizsgáljuk azt a síkgráfot, melynek csúcsai a háromszögek csúcsai, és élei a háromszögek oldalainak azon darabjai, melyek közvetlenül szomszédos csúcsokat kötnek össze. Legyen a háromszögek száma \(\displaystyle \ell\), a gráf csúcsainak és éleinek száma \(\displaystyle c\) és \(\displaystyle e\).
\(\displaystyle (1)\) Euler képlete szerint \(\displaystyle c-e+\ell=1\).
\(\displaystyle (2)\) Számoljuk össze a szögeket: egyrészt a szögek összege \(\displaystyle \ell \pi\), másrészt minden belső csúcsnál a szögek összege mindig \(\displaystyle \pi\) vagy \(\displaystyle 2\pi\), tehát
\(\displaystyle \ell\pi \ge (c-n)\pi +(n-2)\pi.\)
\(\displaystyle (3)\) Számoljuk össze az oldalakat: ha egy háromszögoldal \(\displaystyle k\) részre van osztva, minden részre írjunk \(\displaystyle \frac1k\) értéket, ekkor egyrészt a felírt számok összege \(\displaystyle 3l\), másrészt a feltétel szerint az \(\displaystyle n\)-szög belsejében a gráf egy élére írt két szám összege \(\displaystyle \le 1+\frac12\) (az \(\displaystyle n\)-szög határán pedig csak egy szám lehet, ami \(\displaystyle \le 1\)). Emiatt
\(\displaystyle 3\ell\le \frac32(e-n)+n\le \frac32(e+1)-\frac72.\)
Befejezés. \(\displaystyle (3)\)-at, majd \(\displaystyle (1)\)-et, majd \(\displaystyle (2)\)-t alkalmazva ellentmondásra jutunk:
\(\displaystyle 2\ell+\frac73\le e+1=c+\ell\le 2\ell+2.\)
Statistics:
7 students sent a solution. 5 points: Bukva Balázs, Gáspár Attila, Imolay András, Matolcsi Dávid, Schrettner Jakab, Weisz Máté. 0 point: 1 student.
Problems in Mathematics of KöMaL, December 2017
