Problem A. 712. (December 2017)

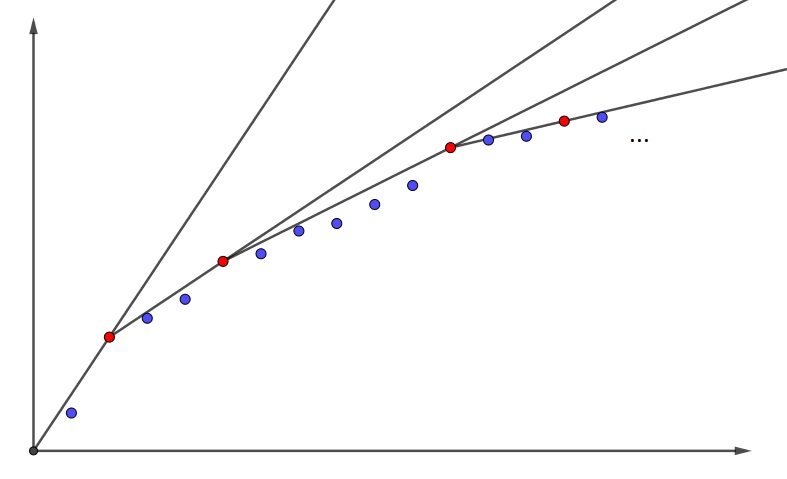
A. 712. We say that a strictly increasing positive real sequence \(\displaystyle a_1,a_2,\dots\) is an elf sequence if for any \(\displaystyle c>0\) we can find an \(\displaystyle N\) such that \(\displaystyle a_n<cn\) for \(\displaystyle n=N,N+1,\dots\,.\) Furthermore, we say that \(\displaystyle a_n\) is a hat if \(\displaystyle a_{n-i}+a_{n+i}<2a_n\) for \(\displaystyle 1\le i\le n-1\). Is it true that every elf sequence has infinitely many hats?

(5 pont)

Deadline expired on January 10, 2018.

Proof without words:

Statistics:

9 students sent a solution.
5 points:	Daróczi Sándor, Gáspár Attila, Imolay András, Janzer Orsolya Lili, Matolcsi Dávid, Schrettner Jakab, Schweitzer Ádám, Szabó Kristóf.
4 points:	Bukva Balázs.

Problems in Mathematics of KöMaL, December 2017