 Problem A. 719. (March 2018)
Problem A. 719. (March 2018)
A. 719. Let \(\displaystyle ABC\) be a scalene triangle with circumcenter \(\displaystyle O\) and incenter \(\displaystyle I\). The \(\displaystyle A\)-excircle, \(\displaystyle B\)-excircle, and \(\displaystyle C\)-excircle of triangle \(\displaystyle ABC\) touch \(\displaystyle BC\), \(\displaystyle CA\), and \(\displaystyle AB\) at points \(\displaystyle A_1\), \(\displaystyle B_1\), and \(\displaystyle C_1\), respectively. Let \(\displaystyle P\) be the orthocenter of \(\displaystyle AB_1C_1\) and \(\displaystyle H\) be the orthocenter of \(\displaystyle ABC\). Show that if \(\displaystyle M\) is the midpoint of \(\displaystyle PA_1\), then lines \(\displaystyle HM\) and \(\displaystyle OI\) are parallel.
Proposed by: Michael Ren, Andover, Massachusetts, USA
(5 pont)
Deadline expired on April 10, 2018.
Sorry, the solution is available only in Hungarian. Google translation
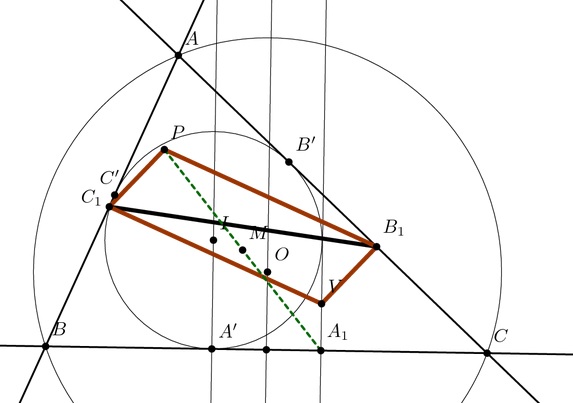
Megoldás. Az \(\displaystyle I\) pont vetülete \(\displaystyle BC,CA,AB\)-re legyen \(\displaystyle A',B',C'\) (ezek a beírt kör érintési pontjai). Ekkor ismert, hogy \(\displaystyle A'\) az \(\displaystyle A_1\) tükörképe \(\displaystyle BC\) felezőpontjára stb., amit abban foglalhatunk össze, hogy \(\displaystyle V\) pont vetülete \(\displaystyle BC,CA,AB\)-re \(\displaystyle A_1,B_1,C_1\), ahol \(\displaystyle V\) az \(\displaystyle I\) tükörképe \(\displaystyle O\)-ra.
A merőlegességek okán \(\displaystyle PB_1VC_1\) paralelogramma, vagyis \(\displaystyle P=B_1+C_1-V\) (ilyen jelölés esetén a pontokat helyvektoraikkal azonosítjuk). Innen
\(\displaystyle M=\frac12(A_1+B_1+C_1-V).\)
(Ez a szimmetria megsejthető, ha meglátjuk egy jó ábrán, hogy \(\displaystyle \overline{A_1P},\overline{B_1Q},\overline{C_1R}\) közös felezőpontban metsz, ahol \(\displaystyle P,Q,R\) az \(\displaystyle AB_1C_1,BC_1A_1,CA_1B_1\) magasságpontja.)
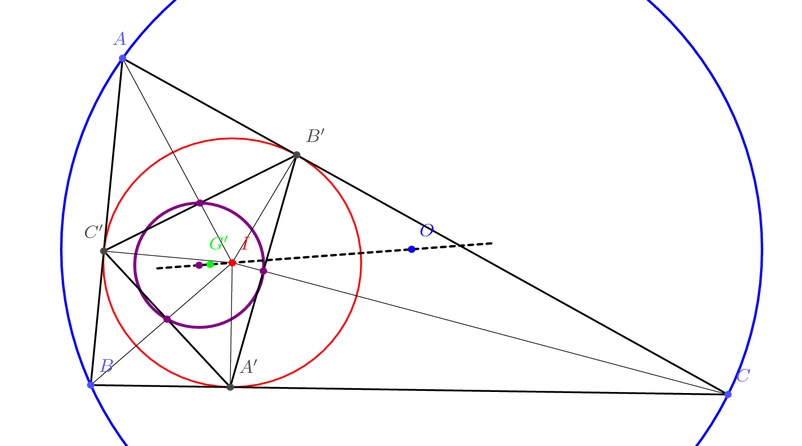
Ismert (a B.4773. feladat következménye, vagy adódik abból, hogy \(\displaystyle A'B'C'\) Feuerbach-körét a beírt körre invertálva, \(\displaystyle ABC\) körülírt körét kapjuk), hogy az \(\displaystyle A'B'C'\) háromszög \(\displaystyle G'\) súlypontja az \(\displaystyle IOV\) egyenes pontja:
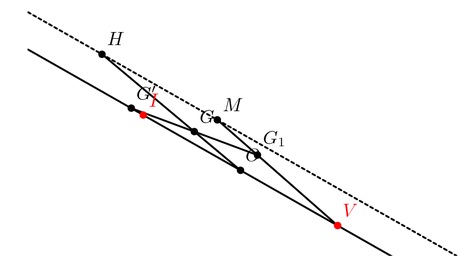
Ha \(\displaystyle G,G_1\) az \(\displaystyle ABC,A_1B_1C_1\) súlypontjai, akkor, mint kibontással ellenőrizhető, \(\displaystyle G=\frac12(G'+G_1)\). Ezért \(\displaystyle d(G_1,IO)=2d(G,IO)\), ahol \(\displaystyle d(\cdot,\cdot)\) jelöli két ponthalmaz minimális távolságát. Azonban \(\displaystyle H-O=3(G-O)\) (arányok Euler-egyenesen) és \(\displaystyle 2(M-V)=3(G_1-V)\) (fenti egyenlőség átrendezése), így
\(\displaystyle d(H,IO)=3\cdot d(G,IO)=\frac32\cdot d(G_1,IO)=d(M,IO),\)
tehát \(\displaystyle HM\) és \(\displaystyle IO\) párhuzamosak.
Megjegyzés. Érdemes meglátni e feladat laza kapcsolódását a B.4790. feladathoz, melyben a három egyenes \(\displaystyle O\)-ra való tükörképei az \(\displaystyle ABC\) magasságpontján haladnak át, mert a magasságpontnak a \(\displaystyle \overline{BC}\) felezőpontjára való tükörképe az \(\displaystyle ABC\) körön \(\displaystyle A\)-val átellenes pont.
Egy másik, ügyes számolást alkalmazó megközelítés, hogy a sík pontjait \(\displaystyle AB,AC\) számegyenesekre való \(\displaystyle u,v\) vetületeik szerint paraméterezzük. Ebben a koordináta-rendszerben levezetve adott irányú egyenes egyenletét, a feladatbeli pontok könnyen számolhatók \(\displaystyle ABC\) oldalainak segítségével (a koszinusztételt felhasználva).
Statistics:
8 students sent a solution. 5 points: Bukva Balázs, Gáspár Attila, Imolay András, Matolcsi Dávid, Szabó Kristóf. 4 points: Márton Dénes. 0 point: 2 students.
Problems in Mathematics of KöMaL, March 2018
