Problem A. 731. (October 2018)

A. 731. Let \(\displaystyle G=(V,E)\) be a tree graph with \(\displaystyle n\) vertices, and let \(\displaystyle P\) be a set of \(\displaystyle n\) points in the plane with no three points collinear. Is it true that for any choice of the graph \(\displaystyle G\) and set \(\displaystyle P\), we can embed \(\displaystyle G\) in \(\displaystyle P\), i.e., we can find a bijection \(\displaystyle f\colon V\to P\) such that when we draw the line segment \(\displaystyle \big[f(x),f(y)\big]\) for all \(\displaystyle (x,y)\in E\), no two such segments intersect each other?

Proposed by Benedek Váli, Szeged

(7 pont)

Deadline expired on November 12, 2018.

Solution. The answer is yes. We will prove the following, stronger statement:

If \(\displaystyle G\) is a tree with \(\displaystyle n\) vertices, with a vertex \(\displaystyle r\) that is designated as root of the graph, and \(\displaystyle P\) is set of \(\displaystyle n\) points in the plane with no three points collinear and \(\displaystyle R\) is a vertex of the convex hall of \(\displaystyle P\) then \(\displaystyle G\) can be embedded in \(\displaystyle P\). (Figure 1).

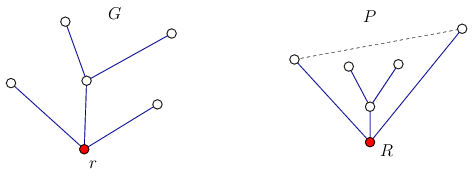
Figure 1

We prove by induction on \(\displaystyle n\). The statement is trivial for \(\displaystyle n=1\). Suppose that \(\displaystyle n\ge2\) and the statement holds true for all smaller values of \(\displaystyle n\).

If we remove the vertex \(\displaystyle r\) from \(\displaystyle G\) then the resulting subgraph \(\displaystyle G'\) splits into some connected components \(\displaystyle G_1,\ldots,G_k\); being connected and circle-free, they are trees. We show that each of these trees contains exactly one neighbour of \(\displaystyle r\).

Consider a component \(\displaystyle G_i\) and select a vertex \(\displaystyle v\) in it. The vertex \(\displaystyle r\) can be connected with \(\displaystyle v\) with some path in \(\displaystyle G\). The first edge in that path connects \(\displaystyle r\) with one of its neighbours \(\displaystyle w\). The other edges of the path lie in \(\displaystyle G'\), so \(\displaystyle v\) and \(\displaystyle w\) lie in the same component of \(\displaystyle G'\), so \(\displaystyle w\) and \(\displaystyle v\) lie in the same component; therefore \(\displaystyle w\in G_i\). (Figure 2)

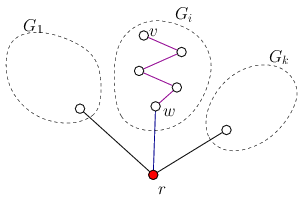
Figure 2

On the other hand, if there were two neighbours \(\displaystyle w_1\) and \(\displaystyle w_2\) of \(\displaystyle r\) in \(\displaystyle G_i\) then they would be connected by some path within \(\displaystyle G'\). But that path and the edges \(\displaystyle (r,w_1)\) and \(\displaystyle (r,w2)\) would form a cycle in \(\displaystyle G\), contradicting the condition that \(\displaystyle G\) is a tree. (Figure 3)

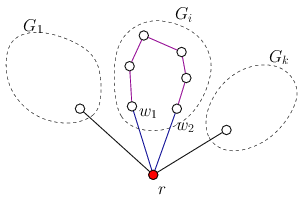
Figure 3

From now on, in each subtree \(\displaystyle G_i\), denote by \(\displaystyle r_i\) the unique neigbour of \(\displaystyle r\).

Since \(\displaystyle R\) is a vertex of the convex hull of \(\displaystyle P\), the other points of \(\displaystyle P\) lie in an angle domain starting at \(\displaystyle R\). Divide this angle domain into \(\displaystyle k\) angles \(\displaystyle D_1,\ldots,D_k\) in such a way that each \(\displaystyle D_i\) contains the same number of points from \(\displaystyle P\) as the number of vertices in \(\displaystyle G_i\). Denote by \(\displaystyle P_i\) the points of \(\displaystyle P\), lying in \(\displaystyle D_i\).

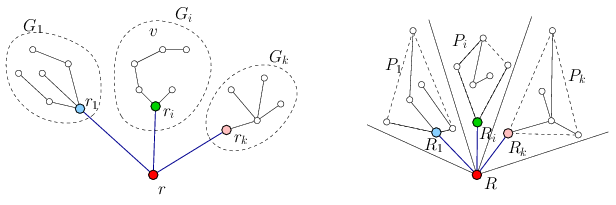
Figure 4

At least one vertex of the convex hull of each \(\displaystyle P_i\) can be connected with \(\displaystyle R\) outside the convex hull; let \(\displaystyle R_i\) be such a point. Draw the line segments \(\displaystyle RR_i\), and apply the induction hypothesis for each tree \(\displaystyle G_i\) with root \(\displaystyle r_i\), and the sets \(\displaystyle P_i\) and the point \(\displaystyle R_i\). This way we obtain a proper embedding of \(\displaystyle G\). (Figure 4)

Statistics:

14 students sent a solution.
7 points:	Beke Csongor, Csaplár Viktor, Milan Haiman, Nagy Nándor, Schrettner Jakab, Szabó 417 Dávid, Tóth 827 Balázs, Weisz Máté.
6 points:	Hegedűs Dániel.
3 points:	2 students.
2 points:	1 student.
1 point:	1 student.
0 point:	1 student.

Problems in Mathematics of KöMaL, October 2018