Problem A. 733. (October 2018)

A. 733. Circle $\displaystyle \omega$ lies in the interior of circle $\displaystyle \Omega$, on which a point $\displaystyle X$ moves. The tangents from $\displaystyle X$ to $\displaystyle \omega$ intersect $\displaystyle \Omega$ for the second time at points $\displaystyle A\ne X$ and $\displaystyle B\ne X$. Prove that the lines $\displaystyle AB$ are either all tangent to a fixed circle, or they all pass through a point.

(7 pont)

Deadline expired on November 12, 2018.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Észrevehetjük, hogy a feladat kapcsolódik a Poncelet-tételhez. Mint Hraskó András cikkében, kulcsötletünk megadni egy "mértéket" az $\displaystyle \Omega$ körön úgy, hogy az $\displaystyle \omega$ kört érintő irányított egyenesekhez tartozó megfelelő ívekhez azonos mérték tartozzék.

Válasszunk koordináta-rendszert, melyben $\displaystyle \Omega$ az egységkör, és paraméterezzük $\displaystyle P_\varphi=(\cos \varphi,\sin\varphi)$ módon. Egy $\displaystyle P\in \Omega$ ponthoz hozzárendelhetjük azt a $\displaystyle Q\in \Omega$ és $\displaystyle T\in \omega$ pontot, melyre $\displaystyle PQ$ $\displaystyle T$-ben érinti $\displaystyle \omega$-t és az $\displaystyle \omega$ kör a $\displaystyle PQ$ irányított egyenes bal félsíkjára esik. (A bal félsík algebrailag a következőképp adható meg: legyen $\displaystyle \overrightarrow{PQ}$ vektor $\displaystyle +90^\circ$-kal való elforgatottja $\displaystyle \mathbb{n}$, ekkor a bal félsík $\displaystyle \{\mathbb{x}:\mathbb{n}\cdot (\mathbb{x}-P)\ge 0\}$.)

Koordináta-geometriai számítással könnyen ellenőrizhető, hogy a $\displaystyle P$-hez $\displaystyle Q$-t ill. $\displaystyle T$-t hozzárendelő függvények folytonosak. Ha $\displaystyle P=P_\varphi$, jelölje $\displaystyle \psi(\varphi)$ azt a szöget, melyre $\displaystyle 0<\psi(\varphi)-\varphi\le 2\pi$ és $\displaystyle Q=P_{\psi(\varphi)}$.

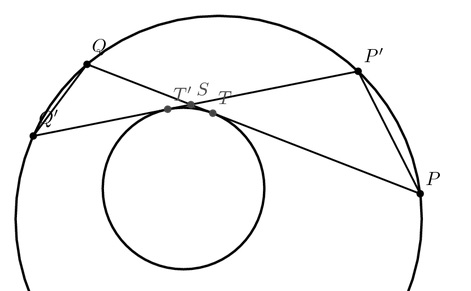
Tekintsünk két ilyen pontot: $\displaystyle P=P_\varphi$ és $\displaystyle P'=P_{\varphi'}$. Tekintsük értelemszerűen a $\displaystyle Q,T$ és $\displaystyle Q',T'$ pontokat. Ha $\displaystyle S=PQ\cap P'Q'$ (elég közeli $\displaystyle P,P'$-re $\displaystyle S$ létezik), akkor a kerületi szögek tételéből belátható $\displaystyle PSP'\sim Q'SQ$, s ezzel

$\displaystyle \frac{QQ'}{PP'}=\frac{Q'S}{SP}.$

Ha $\displaystyle \varphi'\to \varphi$ (azaz: ha $\displaystyle \varphi'$ helyére egy $\displaystyle \varphi$-hez konvergáló sorozat tagjait írjuk), akkor $\displaystyle T'\to T$-ből belátható $\displaystyle S\to T$, s így $\displaystyle Q'\to Q$ miatt $\displaystyle \frac{Q'S}{SP}\to \frac{QT}{TP}$. Másrészt, a szinusztétel miatt

$\displaystyle \frac{QQ'}{PP'}=\frac{2\sin\frac{\psi(\varphi')-\psi(\varphi)}{2}}{2\sin \frac{\varphi'-\varphi}{2}},$

ezért $\displaystyle \frac{QQ'}{PP'}\to \frac{QT}{TP}$-ből az ismert $\displaystyle \lim_{x\to 0}\frac{\sin x}{x}=0$ összefüggés segítségével $\displaystyle \frac{\psi(\varphi')-\psi(\varphi)}{\varphi'-\varphi}\to \frac{QT}{TP}$ következik. A derivált definíciója szerint így

$\displaystyle \frac{d\psi}{d\varphi}=\frac{QT}{TP}.$

Ha az $\displaystyle (u,v)$ középpontú, $\displaystyle r$ sugarú $\displaystyle k$ kör egyenletét $\displaystyle k(x,y)=(x-u)^2+(y-v)^2-r^2=0$ alakban adjuk meg, akkor a Pitagorasz-tétel szerint egy $\displaystyle P$ külső pontjára $\displaystyle k(P)$ a $\displaystyle P$-ből a körhöz húzható érintő hosszának négyzetét adja meg. Ily módon

$\displaystyle \frac{d\psi}{d\varphi}=\frac{\sqrt{\omega(P_{\psi(\varphi)})}}{\sqrt{\omega(P_\varphi)}}.$

Most tekintsük az $\displaystyle f(P)=\frac1{\sqrt{\omega(P)}}$ "eloszlást", ami folytonos függvény. Az $\displaystyle [\alpha,\beta]$ által paraméterezett ív "mértéke" pedig legyen $\displaystyle \int_{\alpha}^\beta f(P_\theta)d\theta$ (folytonosság miatt az integrál létezik). A $\displaystyle PQ$ ív mértéke ($\displaystyle P=P_\varphi$) ekkor:

$\displaystyle I(\varphi)=\int_{\varphi}^{\psi(\varphi)} f(P_\theta)d\theta$

A függvény konstans, hisz differenciálva:

$\displaystyle \frac{dI}{d\varphi}=f(\psi(\varphi))\frac{d\psi}{d\varphi}-f(\varphi)=0.$

Tehát az $\displaystyle \Omega$ körnek $\displaystyle \omega$-t érintő húrjaihoz tartozó ívek mértéke mindig egy adott $\displaystyle I$ érték. Sőt, $\displaystyle I$ mértékű ív csak $\displaystyle [\varphi,\psi(\varphi)]$ által paraméterezett ív lehet.

A megoldás kulcsa az az észrevétel, hogy ha a $\displaystyle \Gamma$ kört a $\displaystyle \Gamma(x,y)=\lambda \omega(x,y)+(1-\lambda)\Omega(x,y)$ egyenlettel definiáljuk (tehát $\displaystyle \omega,\Omega,\Gamma$ egy körsorra esnek), akkor $\displaystyle P\in \Omega$-ra $\displaystyle \Gamma(P)=\lambda\omega(P)$, így $\displaystyle \lambda>0$-ra $\displaystyle \Gamma$ az $\displaystyle \Omega$ belsejébe esik. Mint láttuk, az $\displaystyle \tilde{f}(P)=\frac1{\sqrt{\Gamma(P)}}$ "eloszlás" mellett a $\displaystyle \Gamma$ kört érintő húrok ívének mértéke állandó. Azonban $\displaystyle \tilde{f}=\lambda^{-1/2}f$, így az $\displaystyle f$ eloszlással is egy $\displaystyle K$ állandó lesz a $\displaystyle \Gamma$ kört érintő húrok mértéke. Sőt, $\displaystyle K$ mértékű ív csak $\displaystyle \Gamma$-t érintő húrhoz tartozhat.

Legyen a teljes $\displaystyle \Omega$ kör mértéke:

$\displaystyle J=\int_{\varphi}^{\varphi+2\pi}f(P_\theta)d\theta.$

Ekkor az $\displaystyle AXB$ háromszög egy adott helyzete esetén (feltéve, hogy $\displaystyle AXB$ pozitív körüljárású), $\displaystyle A=P_\varphi$ esetén az $\displaystyle \Omega$ kört $\displaystyle [\varphi,\varphi+2\pi]$-vel paraméterezve: $\displaystyle X=P_{\psi(\varphi)}$, $\displaystyle B=P_{\psi(\psi(\varphi))}$, és

$\displaystyle J=\int_{\varphi}^{\psi(\varphi)}f(P_\theta)d\theta+\int_{\varphi}^{\psi(\psi(\varphi))}f(P_\theta)d\theta+\int_{\psi(\psi(\varphi))}^{\varphi+2\pi}f(P_\theta)d\theta.$

Tehát $\displaystyle BA$ ív mértéke $\displaystyle X$ bármely helyzetére $\displaystyle J-2I>0$. Mivel $\displaystyle \Omega$ bármely $\displaystyle BA$ ívéhez található $\displaystyle \Gamma$ a körsoron, melyre $\displaystyle BA$ (jobbról) érinti $\displaystyle \Gamma$-t, így egy adott $\displaystyle BA$-hoz szerkesztve $\displaystyle \Gamma$-t, $\displaystyle K=J-2I$ adódik. Ekkor pedig $\displaystyle X$ bármely helyzetére az $\displaystyle AB$ egyenes érinti $\displaystyle \Gamma$ kört.

Schrettner Jakab megoldása alapján

Statistics:

4 students sent a solution.
7 points:	Schrettner Jakab.
6 points:	Milan Haiman.
1 point:	1 student.
0 point:	1 student.

Problems in Mathematics of KöMaL, October 2018