 Problem A. 736. (November 2018)
Problem A. 736. (November 2018)
A. 736. Let \(\displaystyle P\) be a point in the plane of triangle \(\displaystyle ABC\). Denote the reflections of \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) about \(\displaystyle P\) by \(\displaystyle A'\), \(\displaystyle B'\) and \(\displaystyle C'\), respectively. Let \(\displaystyle A''\), \(\displaystyle B''\), \(\displaystyle C''\) be the reflections of \(\displaystyle A'\), \(\displaystyle B'\), \(\displaystyle C'\) over the lines \(\displaystyle BC\), \(\displaystyle CA\) and \(\displaystyle AB\), respectively. Let the line \(\displaystyle A''B''\) intersect \(\displaystyle AC\) at \(\displaystyle A_b\) and let \(\displaystyle A''C''\) intersect \(\displaystyle AB\) at a point \(\displaystyle A_c\). Denote by \(\displaystyle \omega_A\) the circle through the points \(\displaystyle A\), \(\displaystyle A_b\), \(\displaystyle A_c\). The circles \(\displaystyle \omega_B\), \(\displaystyle \omega_C\) are defined similarly. Prove that \(\displaystyle \omega_A\), \(\displaystyle \omega_B\), \(\displaystyle \omega_C\) are coaxial, i.e., they share a common radical axis.
Proposed by Navneel Singhal, Delhi and K. V. Sudharshan, Chennai, India
(7 pont)
Deadline expired on December 10, 2018.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Feltesszük, hogy a feladatban megadott pontok mind különbözőek. Mivel \(\displaystyle AA_b\) az \(\displaystyle AC\), \(\displaystyle AA_c\) az \(\displaystyle AB\) egyenessel esik egybe, a három pont nem egy egyenesre illeszkedik, így valóban egy kört határoz meg.
A feladat geometriai tartalma az alábbi állítás.
Állítás. \(\displaystyle ABC\) és \(\displaystyle A''B''C''\) háromszögek hasonlóak és ellentétes körüljárásúak.
Bizonyítás. Az \(\displaystyle ABC\) körülírt körének \(\displaystyle O\) középpontját érdemes kijelölni: mint egy ábráról megsejthető, \(\displaystyle O\) az \(\displaystyle A''B''C''\) kör középpontja is.
Ha az \(\displaystyle \overrightarrow{OA''}\)-t a \(\displaystyle BC\)-re tükrözzük, az \(\displaystyle \overrightarrow{O_AA'}\) adódik, ahol \(\displaystyle O_A\) az \(\displaystyle O\) tükörképe \(\displaystyle BC\)-re. Hasonlóan, \(\displaystyle \overrightarrow{OB''}\) tükörképe \(\displaystyle AC\)-re \(\displaystyle \overrightarrow{O_BB'}\). Belátjuk, hogy ez a két vektor azonos: \(\displaystyle \overrightarrow{O_AA'}=\overrightarrow{O_BB'}=:\mathbb{v}\). (Innen például \(\displaystyle OA''=OB''\).)
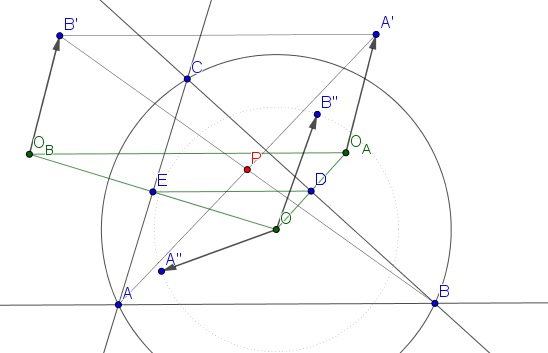
Legyen \(\displaystyle BC\) és \(\displaystyle AC\) felezőpontja \(\displaystyle D\) és \(\displaystyle E\). Ekkor \(\displaystyle D,E\) éppen \(\displaystyle O\) vetülete \(\displaystyle BC,AC\)-re, mert \(\displaystyle O\) a megfelelő oldalak felezőmerőlegesére illeszkedik. Emiatt \(\displaystyle O\)-ból \(\displaystyle 2\)-szeres nagyítással \(\displaystyle \overrightarrow{O_AO_B}=2\overrightarrow{DE}\). Mivel \(\displaystyle DE\) középvonal \(\displaystyle ABC\)-ben, \(\displaystyle 2\overrightarrow{DE}=-\overrightarrow{AB}\). A \(\displaystyle P\)-re tükrözés miatt \(\displaystyle -\overrightarrow{AB}=\overrightarrow{A'B'}\). Tehát \(\displaystyle \overrightarrow{O_AO_B}=\overrightarrow{A'B'}\), amit átrendezve: \(\displaystyle \overrightarrow{O_AA'}=\overrightarrow{O_BB'}\).
A tükrözések miatt
\(\displaystyle \sphericalangle(\mathbb{v},\overrightarrow{OA''})=2\sphericalangle(\mathbb{v},\overrightarrow{CB}),\qquad \sphericalangle(\mathbb{v},\overrightarrow{OB''})=2\sphericalangle(\mathbb{v},\overrightarrow{CA}).\)
Ezeket kivonva egymásból:
\(\displaystyle \sphericalangle(\overrightarrow{OA''},\overrightarrow{OB''})=2\sphericalangle(\overrightarrow{CB},\overrightarrow{CA})=-\sphericalangle(\overrightarrow{OA},\overrightarrow{OB}),\)
ahol utóbbi egyenlőségben a kerületi és középponti szögek tételét alkalmaztuk. A gondolatmenetet az összes lehetséges csúcspárra elvégezve megkapjuk, hogy \(\displaystyle A''B''C''\) háromszög körülírt körének középpontja \(\displaystyle O\), és középponti szögei olyanok, hogy \(\displaystyle ABC\)-hez hasonló s vele ellentétes állású legyen. \(\displaystyle \blacksquare\)
Ezt követően számításos módszereket fogunk kidolgozni, majd azokat alkalmazzuk.
Ha egy \(\displaystyle (u,v)\) középpontú, \(\displaystyle r\) sugarú kör egyenletét a koordináta-síkon felírhatjuk
\(\displaystyle k(x,y)=(x-u)^2+(y-v)^2-r^2=0\)
alakban, tehát egy \(\displaystyle k(x,y)\) polinom segítségével. A sík bármely \(\displaystyle P\) pontjának koordinátáit behelyettesítve, a \(\displaystyle P\) pont \(\displaystyle k\)-ra vonatkozó hatványát kapjuk, a \(\displaystyle k(P)\) mennyiséget. Ezt az euklideszi geometriával (melynek módszerei: szakaszok, szögek, hasonlóság, arányok vizsgálata, illetve körzős-vonalzós szerkesztés) a szelőtétel köti össze: ha egy \(\displaystyle P\)-n áthaladó egyenes az \(\displaystyle A\) és \(\displaystyle B\) pontokban metszi a \(\displaystyle k\) kört, akkor
\(\displaystyle k(P)=\overrightarrow{PA}\cdot \overrightarrow{PB},\)
ahol a szorzat előjelességét vektoros felírással hangsúlyoztuk. Azt fogjuk belátni, hogy alkalmas \(\displaystyle \lambda\) valós számmal
\(\displaystyle \omega_B(x,y)-\lambda \omega_C(x,y)=0\)
teljesül \(\displaystyle A,A_b,A_c\) pontokra. Ekkor ugyanis az \(\displaystyle A,A_b,A_c\) pontok mind teljesítik az
\(\displaystyle \big(\omega_B(x,y)-\omega_A(x,y)\big)-\lambda\big(\omega_C(x,y)-\omega_A(x,y)\big)=0\)
egyenletet, ami \(\displaystyle Kx+Ly+M=0\) alakú. Mivel \(\displaystyle A,A_b,A_c\) nem egy egyenesre illeszkedik, így ebből \(\displaystyle K=L=M=0\) következik, tehát az egyenlet formális azonosság. Mivel pedig \(\displaystyle k\) és \(\displaystyle \ell\) körök hatványvonalának egyenlete \(\displaystyle k(x,y)-\ell(x,y)=0\), ezért emiatt \(\displaystyle \omega_A,\omega_B\) és \(\displaystyle \omega_A,\omega_C\) hatványvonala egybeesik (ennek megállapításához \(\displaystyle \lambda\neq 0\) is kell: \(\displaystyle \omega_A\neq \omega_B\), mert a két kör más pontpárokban metszi az \(\displaystyle AB\) egyenest). A hatványok megegyezése miatt ez \(\displaystyle \omega_B,\omega_C\) hatványvonala is, így a három körnek közös hatványvonala lesz.
Az \(\displaystyle A,A_b,A_c\) pontok \(\displaystyle \omega_B\)-re és \(\displaystyle \omega_C\)-re vonatkozó hatványai pedig könnyen felírhatók:
\(\displaystyle \omega_B(A)=\overrightarrow{AB}\cdot \overrightarrow{AB_c},\qquad\qquad \omega_C(A)=\overrightarrow{AC}\cdot \overrightarrow{AC_b} \)
\(\displaystyle \omega_B(A_b)=\overrightarrow{A_bB_a}\cdot \overrightarrow{A_bB''},\qquad\qquad \omega_C(A_b)=\overrightarrow{A_bC}\cdot \overrightarrow{A_bC_b} \)
\(\displaystyle \omega_B(A_c)=\overrightarrow{A_cB}\cdot \overrightarrow{A_cB_c},\qquad\qquad \omega_C(A_c)=\overrightarrow{A_cC_a}\cdot \overrightarrow{A_cC''}.\)
Elég tehát belátnunk, hogy
| \(\displaystyle \frac{\omega_B(A)}{\omega_C(A)}=\frac{\omega_B(A_b)}{\omega_C(A_b)}\) | \(\displaystyle (1)\) |
(a nevezők nyilván nem nullák), hiszen akkor ugyanezt az okfejtést \(\displaystyle ABC\) helyett \(\displaystyle ACB\) háromszögre elvégezve \(\displaystyle \frac{\omega_C(A)}{\omega_B(A)}=\frac{\omega_C(A_c)}{\omega_B(A_c)}\) adódik, ezért \(\displaystyle A,A_b,A_c\)-nek \(\displaystyle \omega_B,\omega_C\)-re vett hatványainak aránya megegyezik s így megadja a kívánt \(\displaystyle \lambda\) számot. Ehhez a szinusztételt fogjuk felhasználni, azonban az ábra lehetséges állásai miatt egy kevéssé ismert előjeles változatával fogunk dolgozni.
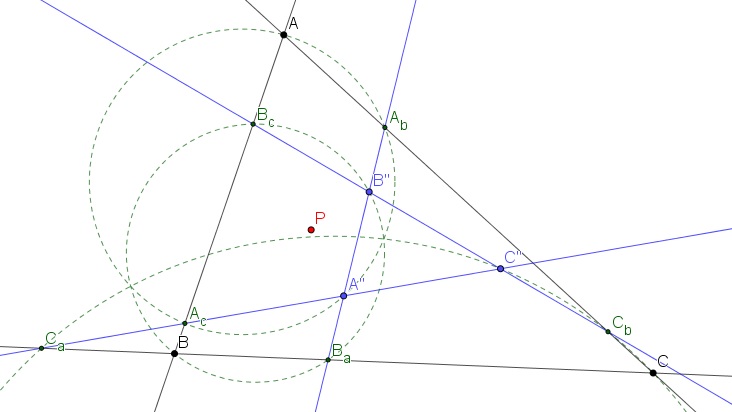
Jelölje a \(\displaystyle BC,CA,AB,B''C'',C''A'',A''B''\) egyeneseket rendre \(\displaystyle a,b,c,a'',b'',c''\), és irányítsuk meg őket! Az \(\displaystyle e\) egyenes megirányítása matematikailag azt jelenti, hogy választunk \(\displaystyle e\)-hez egy \(\displaystyle e\)-vel párhuzamos \(\displaystyle \mathbb{e}\) egységvektort. Ekkor ha \(\displaystyle X,Y\in e\), akkor az \(\displaystyle XY\) irányított távolság az a valós szám, melyre \(\displaystyle \overrightarrow{XY}=XY\cdot \mathbb{e}\).
A szinusztételt az euklideszi geometriában körbe írt háromszögre (is) szokás bizonyítani, azonban ezúttal irányított egyenesekre vonatkozó tételként bizonyítjuk. Definiáljuk az \(\displaystyle a\) és \(\displaystyle b\) irányított egyenesekre az \(\displaystyle \mathbb{a},\mathbb{b}\) irányvektorok segítségével az
\(\displaystyle \sin(ab)=a_1b_2-a_2b_1\)
mennyiséget. A szinusz addíciós képletéből adódóan ez az \(\displaystyle \mathbb{a},\mathbb{b}\) által bezárt forgásszög szinusza: ha \(\displaystyle \mathbb{a}=(\cos\alpha,\sin\alpha)\) és \(\displaystyle \mathbb{b}=(\cos\beta,\sin\beta)\) valamilyen \(\displaystyle \alpha,\beta\in\mathbb{R}\)-re, akkor \(\displaystyle \sin(ab)=\sin(\beta-\alpha)\). Hogyha pedig síkunkat a \(\displaystyle z=0\) síkként \(\displaystyle \mathbb{R}^3\)-be ültetjük, ez éppen az \(\displaystyle \mathbb{a}\times \mathbb{b}\) vektoriális szorzat \(\displaystyle z\)-koordinátája. Ily módon \(\displaystyle a,b,c\) irányított egyenesek esetén a szinusztétel az alábbi módon nyerhető (\(\displaystyle A=b\cap c,B=c\cap a,C=a\cap b\)):
\(\displaystyle \mathbb{0}=\mathbb{a}\times \overrightarrow{BC}=\mathbb{a}\times \left(\overrightarrow{AC}-\overrightarrow{AB}\right)=\mathbb{a}\times (AC\cdot \mathbb{b})-\mathbb{a}\times (AB\cdot \mathbb{c}),\)
melyben a harmadik koordinátákat leolvasva:
\(\displaystyle 0=AC\sin(ab)-AB\sin(ac),\qquad \text{azaz}\qquad \frac{\sin(ab)}{\sin(ac)}=\frac{AB}{AC}.\)
(Talán elegánsabban látszik a szimmetria, ha területvektorral ügyeskedünk:
\(\displaystyle -AB\cdot AC\cdot (\mathbb{b}\times \mathbb{c}) =\overrightarrow{AB}\times \overrightarrow{AC}=(B-A)\times (C-A)=A\times B+B\times C+C\times A.)\)
Mivel a megfelelő szakaszok irányított egyeneseinkre esnek, \(\displaystyle (1)\)-et előjeles szakaszokkal kiírhatjuk:
| \(\displaystyle \frac{AB\cdot AB_c}{AC\cdot AC_b}=\frac{A_bB_a\cdot A_bB''}{A_bC\cdot A_bC_b}.\) | \(\displaystyle (2)\) |
Szinusztételeket felírva:
\(\displaystyle \frac{AB}{AC}=\frac{\sin(ab)}{\sin(ac)},\quad \frac{AB_c}{AC_b}=\frac{\sin(a''b)}{\sin(a''c)},\quad \frac{A_bB_a}{A_bC}=\frac{\sin(ab)}{\sin(ac'')},\quad \frac{A_bB''}{A_bC_b}=\frac{\sin(a''b)}{\sin(a''c'')}.\)
A \(\displaystyle (2)\)-be mindezt beírva, már csupán annyit kell belátnunk, hogy
| \(\displaystyle \sin(ac)\sin(a''c)=\sin(ac'')\sin(a''c'').\) | \(\displaystyle (3)\) |
Ha \(\displaystyle \sin(xy)\) kifejezésben \(\displaystyle x\) vagy \(\displaystyle y\) egyenes irányítását megfordítjuk, akkor \(\displaystyle \sin(t+\pi)=-\sin t\) okán a kifejezés előjelet vált: emiatt \(\displaystyle (3)\) teljesülése nem függ az egyenesek irányításától. A \(\displaystyle (3)\) azonosság pedig igaz, ha \(\displaystyle \mathbb{a},\mathbb{c},\mathbb{a''},\mathbb{c''}\) rendre \(\displaystyle \theta,\theta+\delta,\varphi,\varphi-\delta\) forgásszöggel paraméterezhető. Ez az azonosság tehát következik abból, hogy \(\displaystyle ABC\) és \(\displaystyle A''B''C''\) hasonló és ellentétes irányítású, és ezzel készen vagyunk.
Statistics:
2 students sent a solution. 7 points: Schrettner Jakab, Weisz Máté.
Problems in Mathematics of KöMaL, November 2018
