 |
Az A. 742. feladat (2019. január) |
A. 742. Az \(\displaystyle \Omega\) körbe írt \(\displaystyle ABCD\) konvex húrnégyszög \(\displaystyle AD\) és \(\displaystyle BC\) oldalegyenesei az \(\displaystyle E\) pontban metszik egymást. Legyen \(\displaystyle M\) és \(\displaystyle N\) a többi csúcsot nem tartalmazó \(\displaystyle AB\), illetve \(\displaystyle CD\) körívek felezőpontja, továbbá legyen \(\displaystyle I\), \(\displaystyle J\), \(\displaystyle K\), és \(\displaystyle L\) rendre az \(\displaystyle ABD\), a \(\displaystyle ABC\), a \(\displaystyle BCD\), illetve a \(\displaystyle CDA\) háromszögbe írt kör középpontja. Messe \(\displaystyle \Omega\) az \(\displaystyle IJM\) és \(\displaystyle KLN\) köröket másodszor az \(\displaystyle U\ne M\), illetve a \(\displaystyle V\ne N\) pontban. Mutassuk meg, hogy az \(\displaystyle E\), \(\displaystyle U\) és \(\displaystyle V\) pontok egy egyenesre illeszkednek.
(7 pont)
A beküldési határidő 2019. február 11-én LEJÁRT.
Megoldásvázlat. A feladat szorosan kapcsolódik az A505 feladat megoldásához: Az A.505. betűzésével \(\displaystyle PT\cdot PG=PA\cdot PB=PO_1\cdot PO_2\), emiatt az \(\displaystyle O_1,O_2,T,G\) egy körön vannak.
Legyen \(\displaystyle \omega_1\) és \(\displaystyle \omega_2\) az a két kör az \(\displaystyle ABCD\) négyszög belsejében, amely érinti az \(\displaystyle AD\) és a \(\displaystyle BC\) oldalakat, valamint a körülírt kör \(\displaystyle AMB\), illetve \(\displaystyle CND\) ívét. A fenti, az A.505. megoldásából leolvasott eremény szerint a két érintési pont \(\displaystyle U\), illetve \(\displaystyle V\).
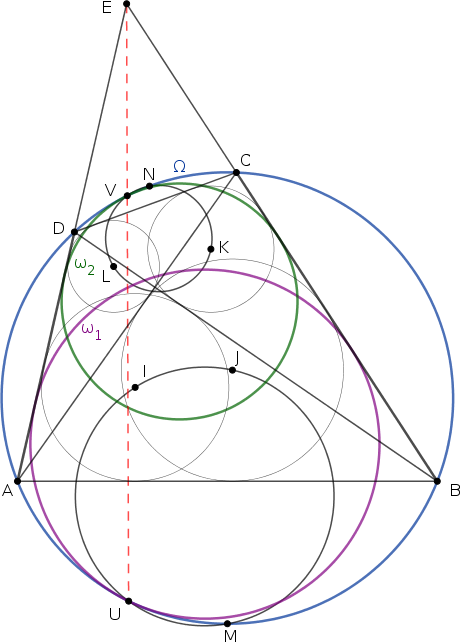
Az \(\displaystyle \Omega\), \(\displaystyle \omega_1\) és \(\displaystyle \omega_2\) körök páronként vett külső hasonlósági pontja \(\displaystyle E\), \(\displaystyle U\) és \(\displaystyle V\); ezek a Monge-tétel szerint egy egyenesre esnek.
Statisztika:
5 dolgozat érkezett. 7 pontot kapott: Schrettner Jakab, Shuborno Das. 3 pontot kapott: 1 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2019. januári matematika feladatai

