Mathematical and Physical Journal
for High Schools
Issued by the MATFUND Foundation
Already signed up?
New to KöMaL?

Problem A. 742. (January 2019)

A. 742. Convex quadrilateral \(\displaystyle ABCD\) is inscribed in circle \(\displaystyle \Omega\). Its sides \(\displaystyle AD\) and \(\displaystyle BC\) intersect at point \(\displaystyle E\). Let \(\displaystyle M\) and \(\displaystyle N\) be the midpoints of the circle arcs \(\displaystyle AB\) and \(\displaystyle CD\) not containing the other vertices, and let \(\displaystyle I\), \(\displaystyle J\), \(\displaystyle K\), \(\displaystyle L\) denote the incentres of triangles \(\displaystyle ABD\), \(\displaystyle ABC\), \(\displaystyle BCD\), \(\displaystyle CDA\), respectively. Suppose \(\displaystyle \Omega\) intersects circles \(\displaystyle IJM\) and \(\displaystyle KLN\) for the second time at points \(\displaystyle U\ne M\) and \(\displaystyle V\ne N\). Show that the points \(\displaystyle E\), \(\displaystyle U\), and \(\displaystyle V\) are collinear.

(7 pont)

Deadline expired on February 11, 2019.

Sorry, the solution is available only in Hungarian. Google translation

Megoldásvázlat. A feladat szorosan kapcsolódik az A505 feladat megoldásához: Az A.505. betűzésével \(\displaystyle PT\cdot PG=PA\cdot PB=PO_1\cdot PO_2\), emiatt az \(\displaystyle O_1,O_2,T,G\) egy körön vannak.

Legyen \(\displaystyle \omega_1\) és \(\displaystyle \omega_2\) az a két kör az \(\displaystyle ABCD\) négyszög belsejében, amely érinti az \(\displaystyle AD\) és a \(\displaystyle BC\) oldalakat, valamint a körülírt kör \(\displaystyle AMB\), illetve \(\displaystyle CND\) ívét. A fenti, az A.505. megoldásából leolvasott eremény szerint a két érintési pont \(\displaystyle U\), illetve \(\displaystyle V\).

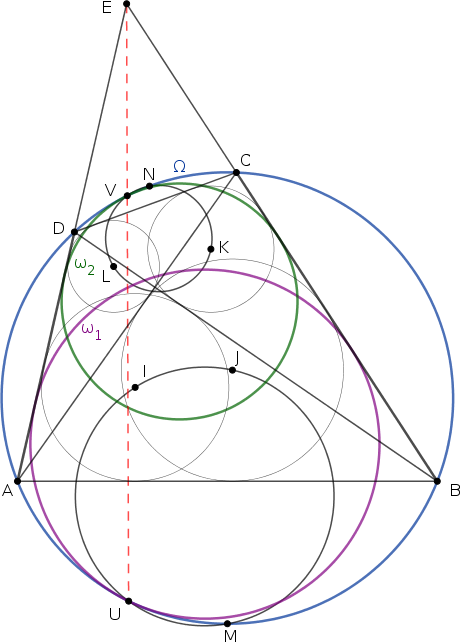
Az \(\displaystyle \Omega\), \(\displaystyle \omega_1\) és \(\displaystyle \omega_2\) körök páronként vett külső hasonlósági pontja \(\displaystyle E\), \(\displaystyle U\) és \(\displaystyle V\); ezek a Monge-tétel szerint egy egyenesre esnek.

Statistics:

5 students sent a solution.
7 points:Schrettner Jakab, Shuborno Das.
3 points:1 student.
0 point:2 students.

Problems in Mathematics of KöMaL, January 2019