Problem A. 745. (February 2019)

A. 745. We have attached a clock hand to every face of a convex polyhedron. Each hand always points towards a neighboring face (two faces of the polyhedron are neighbors if they share an edge). At the end of every minute, exactly one of the hands turns clockwise to point at the next face. Suppose that the hands on neighboring faces never point towards one another. Show that one of the hands makes only finitely many turns.

(7 pont)

Deadline expired on March 11, 2019.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A poliéder lapjai legyenek: \(\displaystyle L_1,L_2,\dots,L_n\). Készítsünk egy irányított gráfot: mondjuk azt, hogy \(\displaystyle L_i\to L_j\), ha az \(\displaystyle L_i\)-n lévő mutató \(\displaystyle L_j\) felé mutat. Akármelyik \(\displaystyle L_i\) lapból is indulunk ki, az élek mentén haladva egy \(\displaystyle L_i\to L_j\to \dots\) lapsorozat képezhető: a skatulya-elv szerint legkésőbb az \(\displaystyle n+1\)-edik lapig kell várnunk, hogy valamelyik lap megismétlődjön. Az első megismételt laptól, \(\displaystyle L_{i_1}\)-től kezdve ekkor \(\displaystyle L_{i_1}\to L_{i_2}\to \dots\to L_{i_k}\to L_{i_1}\to \dots\) módon ciklus ismétlődik. A feladat feltétele, hogy szomszédos lapok mutatói sosem mutatnak egymás felé, vagyis minden ciklus hossza \(\displaystyle k\ge 3\). Tegyük fel, hogy ezt a feltételt tartva végtelen sokszor elforgatható mindegyik mutató.

(Ötlet. Célunk egy monovariáns keresése lesz: ha például be tudnánk látni, hogy a ciklusok száma minden mutató-elfordulás során csökken, ellentmondásra jutnánk. Olyan jellegű állításokból próbáljuk mozaikként összeállítani a bizonyítást, mint "a legkisebb ciklus mérete nem növekedhet, és ha nem csökken, a második legkisebb ciklus csökken, stb.")

Egy ciklus meghatároz két zárt töröttvonalat, a következő módon. Ha a ciklusban \(\displaystyle L_i\to L_j\), akkor az \(\displaystyle L_i\cap L_j\) élnek az órajárás kitünteti bal és jobb csúcsát (az \(\displaystyle L_i\) mutatója a jobb csúcs felé fordul el). Ha a ciklusban \(\displaystyle L_i\to L_j\to L_k\), akkor \(\displaystyle L_j\) határa mentén kössük össze a két jobb illetve a két bal csúcsot! Ily módon létrejön a ciklus "jobb határa" és "bal határa" (itt a jobb határ alatt élek előbbi módon meghatározott sorozatát értjük, nem pedig azok unióját). Vizsgáljunk most a ciklusba nem eső lapokon haladó töröttvonalakat! Minden, a ciklusba nem eső lap összeköthető a jobb és bal határ valamelyikével, de csak az egyik határral (ez a sokszögekre vonatkozó Jordan-tételből adódik, ám ennek levezetését a versenyben nem vártuk el). Ily módon létrejön a ciklus "jobb felszíne" és "bal felszíne".

Mozgassunk el egy ciklusban egy óramutatót! Definíció szerint a mutató a jobb határ felé fog elmozdulni. A mutató így vagy (1) a ciklus egy későbbi lapja felé fog mutatni (ezzel a jobb felszín megmarad, de a ciklusba eső lapok száma csökken), vagy pedig a jobb felszín egy lapja felé fog mutatni. Utóbbi esetben az irányított gráfon sétálva, vagy (2) a jobb felszínben egy ciklusba jutunk, vagy pedig (3) a jobb felszínből újra ciklusunkba érkezünk, méghozzá úgy, hogy a keletkező ciklus jobb felszíne az eredeti jobb felszín valódi részhalmaza.

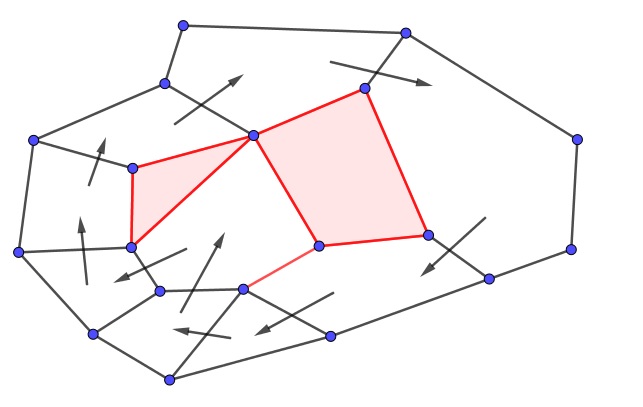
Elképzelhető azonban, hogy a (2) esetben a jobb felszínben talált "kisebb" ciklus "ellentétes irányú", pontosabban hogy e ciklusnak nem bal, hanem jobb felszíne az, ami az eredeti ciklus bal felszínét lefedi. Emiatt szerencsés lesz bevezetni a minimális és maximális ciklus fogalmát: egy ciklus minimális, ha jobb felszínében nincsen ciklus, és maximális, ha bal felszínében nincsen ciklus.

Vizsgáljunk meg egy \(\displaystyle C\) minimális ciklust! Már láttuk, hogy egy \(\displaystyle C\)-re eső mutató elfordulásakor (1) vagy (3) esetén új ciklus alakul ki, ami ismét minimális, hisz jobb felszínében nem lehet ciklus (a (2) esetet kizárja a minimalitás). Ha \(\displaystyle C\) bal felszínén fordul el mutató, a ciklus minimális marad. Ha \(\displaystyle C\) jobb felszínén fordul el mutató, akkor \(\displaystyle C\) vagy minimális marad, vagy pedig létrejön egy új \(\displaystyle C'\) ciklus, mely a mutatót tartalmazza és a jobb felszínbe esik.

Lássuk be, hogy ekkor \(\displaystyle C'\) jobb felszíne \(\displaystyle C\) jobb felszínébe esik! Figyeljük meg, hogy ha \(\displaystyle L_i\) mutatóját elforgatva jött létre \(\displaystyle C'\), akkor \(\displaystyle L_i\) eredetileg \(\displaystyle C'\) bal határa felé mutatott. Eredetileg \(\displaystyle L_i\)-ből sétát indítva, \(\displaystyle C\)-be kellett jutnunk (hisz nem volt ciklus \(\displaystyle C\) jobb felszínében), így \(\displaystyle C\) lapjai \(\displaystyle C'\) bal felszínében kell legyenek. Ezt akartuk belátni.

Tehát egy minimális ciklus és jobb felszíne szerencsésen viselkedik: ha egy ciklus "mérete" a ciklusba és jobb felszínébe eső lapok összes száma, a legkisebb méretű minimális ciklus mérete vagy csökken, vagy a ciklussal együtt megmarad. Ellentmondásra jutunk tehát, ha van minimális ciklus, hiszen minden mutatót végtelen sokszor kell mozgatnunk.

Mindenképp igaz, hogy van ciklus. Ha az nem minimális, van a jobb felszínében ciklus. E ciklus jobb vagy bal felszíne valódi részhalmaza az előbb tekintett jobb felszínnek: válasszunk abban ciklust stb. Ezzel az eljárással találhatunk minimális vagy maximális ciklust. Tegyük most fel, hogy csak maximális ciklus található.

Legyen \(\displaystyle C\) maximális ciklus! Egy \(\displaystyle C\)-re eső mutató elfordulásakor (1) vagy (2) vagy (3) esetében új ciklus alakul ki \(\displaystyle C\) helyett, ami vagy kisebb méretű, vagy esetleg már nem maximális. Továbbá, ami lényeges, más módon nem is jöhet létre \(\displaystyle C'\) maximális ciklus. A mutató ugyanis eredetileg \(\displaystyle C'\) bal határa felé mutat, s így a mutatóból az eredeti helyzetben sétálva, \(\displaystyle C'\)-be vissza kell jutnunk, hisz egyéb esetben találtunk \(\displaystyle C\) bal felszínében egy ciklust – eredetileg tehát a mutató egy \(\displaystyle C\) ciklusban volt, ami maximális volt, mert \(\displaystyle C'\) maximális és tágabb a bal felszíne ("a maximális ciklus olyan, mint a minimális, ha az időt megfordítjuk"). Ebből következik, hogy a maximális ciklusok méreteinek összege csökken vagy megmarad, s mivel minden mutatót végtelen sokszor kell mozgatnunk, ez az összeg idővel nullára csökken, amely esetben már van minimális ciklus, és készen vagyunk.

Statistics:

2 students sent a solution.
5 points:	1 student.
2 points:	1 student.

Problems in Mathematics of KöMaL, February 2019