 |
Az A. 750. feladat (2019. április) |
A. 750. Legyen \(\displaystyle k_1,\ldots,k_5\) öt kör a síkban úgy, hogy \(\displaystyle k_1\) és \(\displaystyle k_2\) kívülről érintik egymást a \(\displaystyle T\) pontban, \(\displaystyle k_3\) és \(\displaystyle k_4\) kívülről érinti a \(\displaystyle k_1\)-et és a \(\displaystyle k_2\)-t is, \(\displaystyle k_5\) az \(\displaystyle U\), illetve a \(\displaystyle V\) pontban kívülről érinti \(\displaystyle k_3\)-at, illetve \(\displaystyle k_4\)-et, továbbá \(\displaystyle k_5\) a \(\displaystyle P\) és a \(\displaystyle Q\) pontban metszi \(\displaystyle k_1\)-et az ábra szerint.
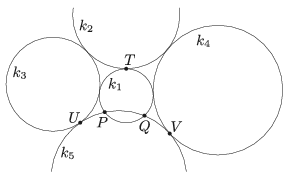
Mutassuk meg, hogy
\(\displaystyle \frac{PU\cdot PV}{QU\cdot QV} = \frac{PT^2}{QT^2}. \)
(7 pont)
A beküldési határidő 2019. május 10-én LEJÁRT.
Megoldás. Az inverzió egyik tipikus alkalmazási módja, hogy köröket egyenesekké transzformálunk, egyszerűsítve az ábrát. Jelen esetben a \(\displaystyle T\) pont körül érdemes inverziót végezni, mondjuk \(\displaystyle h\) hatvánnyal (vagyis: irányított szakaszokkal \(\displaystyle TX\cdot TX'=h\)).
A \(\displaystyle k_1\) és \(\displaystyle k_2\) körök képei egyenesek, amik nem metszőek, így párhuzamosak. A \(\displaystyle k_3'\) és \(\displaystyle k_4'\) körök érintik \(\displaystyle k_1'\) és \(\displaystyle k_2'\) egyeneseket, így középpontjaik egyenlő távol esnek a két egyenestől s ezzel sugaruk egyenlő. A \(\displaystyle k_5'\) kör érinti \(\displaystyle k_3',k_4'\) kört \(\displaystyle U',V'\) pontban és metszi \(\displaystyle k_2'\) egyenest \(\displaystyle P',Q'\)-ben. Az érintés miatt ha \(\displaystyle O_3,O_4,O_5\) jelöli \(\displaystyle k_3',k_4',k_5'\) középpontjait, \(\displaystyle O_5O_3=O_5O_4\), vagyis \(\displaystyle k_5'\) szimmetrikus \(\displaystyle \overline{O_3O_4}\) felezőmerőlegesére nézve. Mivel \(\displaystyle O_3O_4\) eközben \(\displaystyle k_1',k_2'\) középpárhuzamosa, a felezőmerőlegesre \(\displaystyle k_2'\) is szimmetrikus, illetve az egyező sugarak miatt \(\displaystyle k_3',k_4'\) egymás tükörképe rá nézve. Így \(\displaystyle P',Q'\) és \(\displaystyle U',V'\) tükörképek!
A szakaszhosszak közötti kapcsolatot egy képlettel teremtjük meg. Ha \(\displaystyle X,Y\) képe az inverzióban \(\displaystyle X',Y'\), akkor \(\displaystyle TX\cdot TX'=h=TY\cdot TY'\) miatt \(\displaystyle TXY\sim TY'X'\) (közös a \(\displaystyle T\)-nél lévő szög és \(\displaystyle \frac{|TX|}{|TY'|}=\frac{|TY|}{|TX'|}\)), s így
\(\displaystyle \frac{|XY|}{|Y'X'|}=\frac{|TX|}{|TY'|},\qquad |XY|=|X'Y'|\cdot \frac{|TX|\cdot |TY|}{|h|}.\)
Behelyettesítve a bizonyítandó azonosságba:
\(\displaystyle \frac{|PU|\cdot |PV|}{|QU|\cdot |QV|}=\frac{|PT|^2}{|QT|^2},\)
\(\displaystyle \frac{|P'U'|\cdot \frac{|TP|\cdot |TU|}{|h|}\cdot |P'V'|\cdot \frac{|TP|\cdot |TV|}{|h|}}{|Q'U'|\cdot \frac{|TQ|\cdot |TU|}{|h|}\cdot |Q'V'|\cdot \frac{|TQ|\cdot |TV|}{|h|}}=\frac{|TP|^2}{|TQ|^2}\)
\(\displaystyle \frac{|P'U'|\cdot |P'V'|}{|Q'U'|\cdot |Q'V'|}=1\)
A kapott azonosság \(\displaystyle P'U'=Q'V'\) és \(\displaystyle P'V'=Q'U'\) miatt igaz (a szakaszok ugyanis tükrösek).
Megjegyzés. A bizonyítandó képlet ekvivalens azzal, hogy a \(\displaystyle T\)-ben húzott közös érintő, \(\displaystyle PQ\), és \(\displaystyle UV\) egy pontban metszenek.
Statisztika:
3 dolgozat érkezett. 7 pontot kapott: Pooya Esmaeil Akhoondy, Schrettner Jakab, Shuborno Das.
A KöMaL 2019. áprilisi matematika feladatai

