Problem A. 750. (April 2019)

A. 750. Let \(\displaystyle k_1,\ldots,k_5\) be five circles in the plane such that \(\displaystyle k_1\) and \(\displaystyle k_2\) are externally tangent to each other at point \(\displaystyle T\), \(\displaystyle k_3\) and \(\displaystyle k_4\) are externally tangent to both \(\displaystyle k_1\) and \(\displaystyle k_2\), \(\displaystyle k_5\) is externally tangent to \(\displaystyle k_3\) and \(\displaystyle k_4\) at points \(\displaystyle U\) and \(\displaystyle V\), respectively, moreover \(\displaystyle k_5\) intersects \(\displaystyle k_1\) at \(\displaystyle P\) and \(\displaystyle Q\), like shown in the figure.

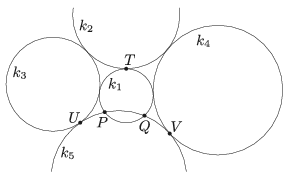
Show that

\(\displaystyle \frac{PU\cdot PV}{QU\cdot QV} = \frac{PT^2}{QT^2}. \)

(7 pont)

Deadline expired on May 10, 2019.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Az inverzió egyik tipikus alkalmazási módja, hogy köröket egyenesekké transzformálunk, egyszerűsítve az ábrát. Jelen esetben a \(\displaystyle T\) pont körül érdemes inverziót végezni, mondjuk \(\displaystyle h\) hatvánnyal (vagyis: irányított szakaszokkal \(\displaystyle TX\cdot TX'=h\)).

A \(\displaystyle k_1\) és \(\displaystyle k_2\) körök képei egyenesek, amik nem metszőek, így párhuzamosak. A \(\displaystyle k_3'\) és \(\displaystyle k_4'\) körök érintik \(\displaystyle k_1'\) és \(\displaystyle k_2'\) egyeneseket, így középpontjaik egyenlő távol esnek a két egyenestől s ezzel sugaruk egyenlő. A \(\displaystyle k_5'\) kör érinti \(\displaystyle k_3',k_4'\) kört \(\displaystyle U',V'\) pontban és metszi \(\displaystyle k_2'\) egyenest \(\displaystyle P',Q'\)-ben. Az érintés miatt ha \(\displaystyle O_3,O_4,O_5\) jelöli \(\displaystyle k_3',k_4',k_5'\) középpontjait, \(\displaystyle O_5O_3=O_5O_4\), vagyis \(\displaystyle k_5'\) szimmetrikus \(\displaystyle \overline{O_3O_4}\) felezőmerőlegesére nézve. Mivel \(\displaystyle O_3O_4\) eközben \(\displaystyle k_1',k_2'\) középpárhuzamosa, a felezőmerőlegesre \(\displaystyle k_2'\) is szimmetrikus, illetve az egyező sugarak miatt \(\displaystyle k_3',k_4'\) egymás tükörképe rá nézve. Így \(\displaystyle P',Q'\) és \(\displaystyle U',V'\) tükörképek!

A szakaszhosszak közötti kapcsolatot egy képlettel teremtjük meg. Ha \(\displaystyle X,Y\) képe az inverzióban \(\displaystyle X',Y'\), akkor \(\displaystyle TX\cdot TX'=h=TY\cdot TY'\) miatt \(\displaystyle TXY\sim TY'X'\) (közös a \(\displaystyle T\)-nél lévő szög és \(\displaystyle \frac{|TX|}{|TY'|}=\frac{|TY|}{|TX'|}\)), s így

\(\displaystyle \frac{|XY|}{|Y'X'|}=\frac{|TX|}{|TY'|},\qquad |XY|=|X'Y'|\cdot \frac{|TX|\cdot |TY|}{|h|}.\)

Behelyettesítve a bizonyítandó azonosságba:

\(\displaystyle \frac{|PU|\cdot |PV|}{|QU|\cdot |QV|}=\frac{|PT|^2}{|QT|^2},\)

\(\displaystyle \frac{|P'U'|\cdot \frac{|TP|\cdot |TU|}{|h|}\cdot |P'V'|\cdot \frac{|TP|\cdot |TV|}{|h|}}{|Q'U'|\cdot \frac{|TQ|\cdot |TU|}{|h|}\cdot |Q'V'|\cdot \frac{|TQ|\cdot |TV|}{|h|}}=\frac{|TP|^2}{|TQ|^2}\)

\(\displaystyle \frac{|P'U'|\cdot |P'V'|}{|Q'U'|\cdot |Q'V'|}=1\)

A kapott azonosság \(\displaystyle P'U'=Q'V'\) és \(\displaystyle P'V'=Q'U'\) miatt igaz (a szakaszok ugyanis tükrösek).

Megjegyzés. A bizonyítandó képlet ekvivalens azzal, hogy a \(\displaystyle T\)-ben húzott közös érintő, \(\displaystyle PQ\), és \(\displaystyle UV\) egy pontban metszenek.

Statistics:

3 students sent a solution.
7 points:	Pooya Esmaeil Akhoondy, Schrettner Jakab, Shuborno Das.

Problems in Mathematics of KöMaL, April 2019