 Problem A. 783. (October 2020)
Problem A. 783. (October 2020)
A. 783. A polyomino is a figure which consists of unit squares joined together by their sides. (A polyomino may contain holes.) Let \(\displaystyle n \ge 3\) be a positive integer. Consider a grid of unit square cells which extends to infinity in all directions. Find, in terms of \(\displaystyle n\), the greatest positive integer \(\displaystyle C\) which satisfies the following condition: For every colouring of the cells of the grid in \(\displaystyle n\) colours, there is some polyomino within the grid which contains at most \(\displaystyle n - 1\) colours and whose area is at least \(\displaystyle C\).
Submitted by Nikolai Beluhov, Stara Zagora, Bulgaria and Stefan Gerdjikov, Sofia, Bulgaria
(7 pont)
Deadline expired on November 10, 2020.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A végtelen négyzetrács akármilyen színezésében megkereshető a lehető legnagyobb területű poliminó, melyben valamelyik szín nem fordul elő.
Létezik olyan színezés, melyben ez az érték éppen
\(\displaystyle 2+4+\dots+2(n-1)+\dots+4+2=n(n-1)+(n-1)(n-2)=2(n-1)^2,\)
az alábbi módon. Az \(\displaystyle y=0\) egyenesen az \(\displaystyle x=0,1,2,\dots,2n-1\)-hez tartozó négyzeteken következzék mind az \(\displaystyle n\) szín kétszer, majd mindkét irányban ismételjük ezt a periódust. Az \(\displaystyle y=0\)-ról \(\displaystyle y=1\)-re lépve, cseréljük meg az \(\displaystyle x\)-edik és \(\displaystyle (x+1)\)-edik négyzet színét minden páratlan \(\displaystyle x\)-re. Az \(\displaystyle y=1\)-ről az \(\displaystyle y=2\)-re lépve, a páros \(\displaystyle x\)-eknél cseréljünk, és így tovább, váltogatva. Álljunk meg az \(\displaystyle y=n-1\) egyenesnél, ugyanis egymás mellé kerül az \(\displaystyle (1,0)\) és \(\displaystyle (2n,0)\) négyzetek színe, és a többi (vízszintesen \(\displaystyle 2\)-t lépve, ugyanazt a mintát látjuk). Ezt az eljárást alkalmazva terjesszük ki mindkét \(\displaystyle y\) irányban a színezést a végtelen négyzetrácsra. Világos, hogy bármely színre az ahhoz tartozó négyzetek \(\displaystyle 2(n-1)^2\) területű összefüggő részeket határolnak körül.
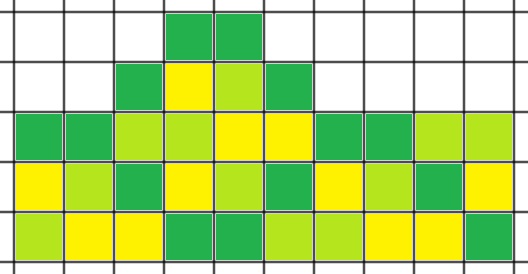
Belátjuk, hogy akárhogyan színezzük a végtelen négyzetrácsot, mindenképpen található egy legalább \(\displaystyle 2(n-1)^2\) területű poliminó, melyben valamelyik szín nem fordul elő.
Mérjük meg egy poliminó "kerületét" a következő különleges módon. A poliminó külső határát vizsgáljuk (amit képezhetünk úgy, hogy vesszük minden sorra és oszlopra a két szélső négyzetének szélét). Rajzoljunk a külső határ mindegyik szakaszára kifelé egy \(\displaystyle 1/4\) területű háromszöget, és szomszédos határmezők esetén még egy-egy háromszöget, az alábbi példákat követve:
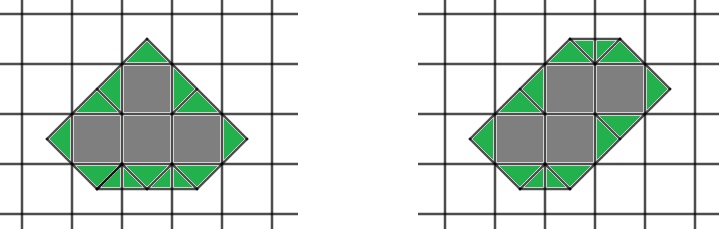
Eredmény. Ha egy \(\displaystyle P\) poliminó területe \(\displaystyle t=t(P)\) és "kerülete" \(\displaystyle k=k(P)\), akkor \(\displaystyle t\le \frac12(k^2+1)\).
Indoklás. Módosítsuk \(\displaystyle P\)-t úgy, hogy közben \(\displaystyle t(P)\) ne csökkenjék és \(\displaystyle k(P)\) ne növekedjék: elegendő az állítást a végül kapott poliminóra ellenőrizni. Először is, vegyük \(\displaystyle P\)-be az általa körülhatárolt négyzeteket. Másodszor pedig, amíg \(\displaystyle P\) határa mentén előfordul az alábbi három határszakasz egyike, toldjunk oda egy négyzetet, az ábrázolt módon:
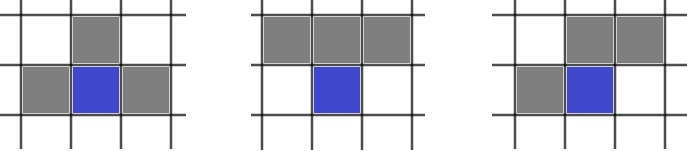
E háromféle lépés a "kerületet" megtartja, míg a területet \(\displaystyle 1\)-gyel növeli. Mivel a terület nem nőhet minden határon túl (a "kerület" legalább akkora, mint az alakzat szélességének negyede), ezért eljutunk egy olyan \(\displaystyle P'\) poliminóhoz, ami nem tartalmaz ilyen határszakaszt. Milyen határa lehet akkor?
A határ menti négyzeteket körüljárva, ha "fel-jobb" irányban lépünk, azután csak "fel-jobb" irányban léphetünk, vagy "fel" irányban, de ha "fel" felé léptünk, onnan csak "fel-bal" irányban folytathatjuk, vagy "bal" irányban, de ha "bal" felé léptünk, váltunk, stb. Tehát átlósan haladva kell körbeérnünk, esetleg egy-egy lépést kivéve mindegyik irányban.
Végül, ha "jobb" és "bal" felé is léptünk, szétvághatjuk a poliminót a "jobb" felé lépés felezőmerőlegesén és \(\displaystyle 1\)-gyel arrébb csúsztatva kiegészíthetjük:
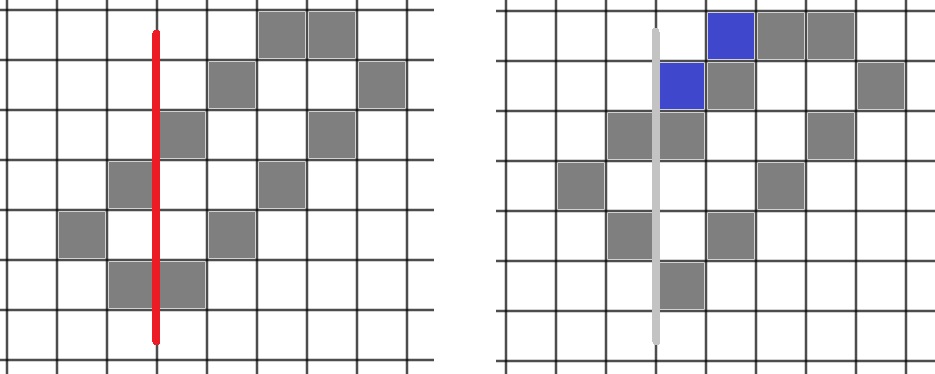
Ezt téve feltehető, hogy "jobb" felé, és hasonlóképp "fel" felé sem lépünk. Kétféle poliminó maradt: egy \(\displaystyle a\times b\)-s ferde rács, vagy egy \(\displaystyle a\times b\)-s ferde rács kiegészítve \(\displaystyle (a-1)\) négyzettel. Alább láthatók ezek \(\displaystyle a=4\), \(\displaystyle b=2\) esetén:
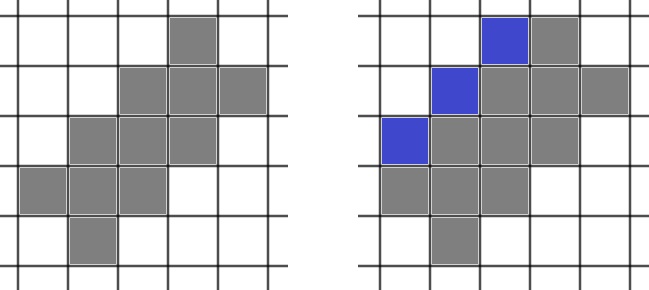
Előbbi esetben \(\displaystyle k=a+b\) és \(\displaystyle t=ab+(a-1)(b-1)=2(a-\frac12)(b-\frac12)+\frac12\). Utóbbi esetben \(\displaystyle k=a+b+\frac12\) és \(\displaystyle t=ab+(a-1)(b-1)+(a-1)=2(a-\frac12)b\). Ha adott két szám összege, akkor legnagyobb a szorzatuk, ha különbségük minimális. Ennek jegyében \(\displaystyle 2t\le k^2+1\) leolvasható. \(\displaystyle \blacksquare\)
Vizsgáljunk most egy \(\displaystyle N\times N\) méretű négyzetrácsot a színezésből. Skatulya-elv miatt valamelyik szín legfeljebb \(\displaystyle \frac1n N^2\)-szer fordul elő. Hagyjuk ki azt a színt, és a megmaradó összefüggő részeket jelölje \(\displaystyle P_1,\dots,P_d\). Világos, hogy
\(\displaystyle \sum_{i=1}^d t(P_i)\ge (1-\frac1n)N^2.\)
Ha \(\displaystyle P_1,\dots,P_d\)-hez még hozzávesszük a "kerületüket", nem lesz köztük átfedés! Mivel az így bővített poliminók együtt lefedhetők egy \(\displaystyle (N+1)^2\) területű négyzettel, kapjuk, hogy
\(\displaystyle \sum_{i=1}^d t(P_i)+k(P_i) \le (N+1)^2.\)
Eredményünk rendezésével \(\displaystyle \frac kt \ge \frac{\sqrt{2t-1}}t\) látható. Az \(\displaystyle u=\sqrt{2t-1}\) helyettesítéssel ellenőrizhető, hogy \(\displaystyle t\)-ben szigorú monoton csökkenő a jobb oldal. Ezért ha \(\displaystyle T=\max \{t(P_1),\dots,t(P_d)\}\), akkor
\(\displaystyle (N+1)^2\ge \sum_{i=1}^d t(P_i)\left(1+\frac{k(P_i)}{t(P_i)}\right)\ge \)
\(\displaystyle \ge \sum_{i=1}^d t(P_i)\left(1+\frac{\sqrt{2T-1}}{T}\right)\ge \left(1+\frac{\sqrt{2T-1}}{T}\right)(1-\frac1n)N^2.\)
Hogyha \(\displaystyle T\le 2(n-1)^2-1\), akkor \(\displaystyle \left(1+\frac{\sqrt{2T-1}}{T}\right)(1-\frac1n)>1\) áll fenn \(\displaystyle n\ge 3\) esetén. Ez elegendően nagy \(\displaystyle N\) esetén ellentmondásos, ezért a végtelen négyzetrácsban található legalább \(\displaystyle 2(n-1)^2\) területű poliminó, melyben valamelyik szín nem fordul elő.
Mindez igazolja, hogy a keresett \(\displaystyle C\) érték \(\displaystyle C=2(n-1)^2\).
Megjegyzés. Hasonló gondolatot alkalmaz ez az amerikai versenyfeladat.
Statistics:
6 students sent a solution. 6 points: Füredi Erik Benjámin. 3 points: 1 student. 2 points: 3 students. 0 point: 1 student.
Problems in Mathematics of KöMaL, October 2020
