Problem A. 809. (November 2021)

A. 809. Let the lengths of the sides of triangle \(\displaystyle ABC\) be denoted by \(\displaystyle a\), \(\displaystyle b\) and \(\displaystyle c\) using the standard notations. Let \(\displaystyle S\) denote the centroid of triangle \(\displaystyle ABC\). Prove that for an arbitrary point \(\displaystyle P\) in the plane of the triangle the following inequality is true:

\(\displaystyle a\cdot PA^3+b\cdot PB^3+c\cdot PC^3\ge 3abc\cdot PS. \)

Proposed by János Schultz, Szeged

(7 pont)

Deadline expired on December 10, 2021.

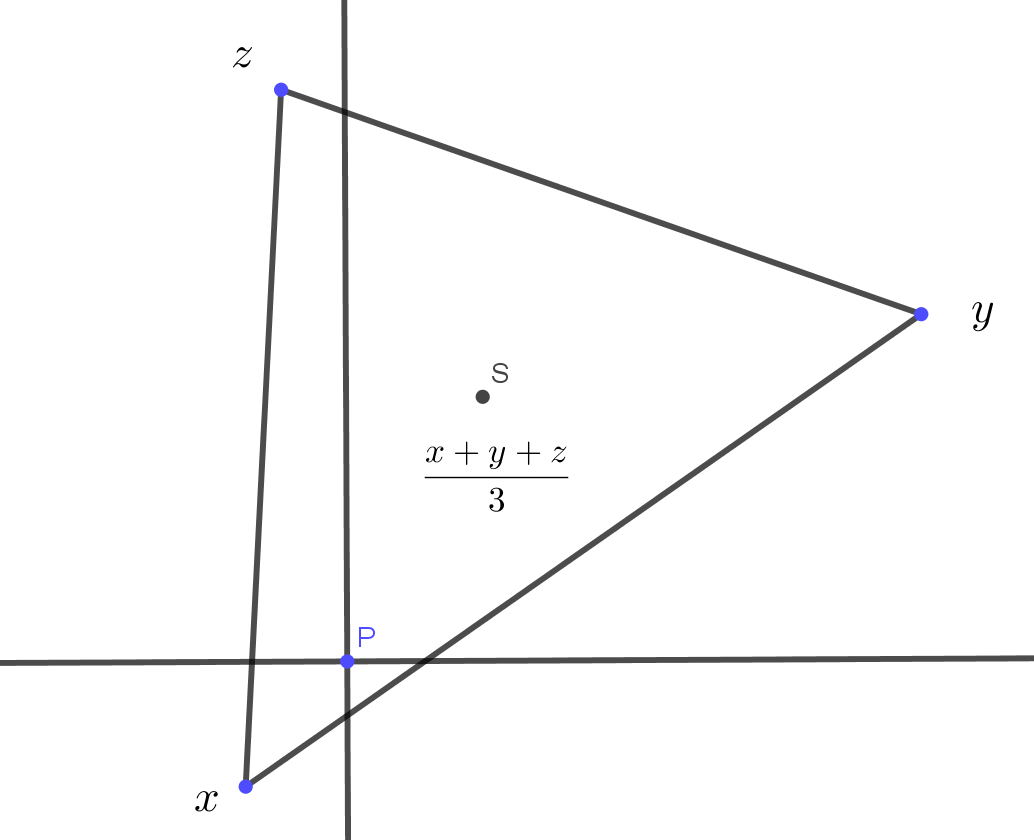
Solution. Let us place the triangle on the complex plane such that \(\displaystyle P\) is the origin. Let \(\displaystyle x\), \(\displaystyle y\) and \(\displaystyle z\) be the complex numbers corresponding to vertices \(\displaystyle A\), \(\displaystyle B\) and \(\displaystyle C\). The complex number corresponding to the centroid is \(\displaystyle \frac{x+y+z}{3}\).

Using these notations the inequality becomes the following:

\(\displaystyle |x|^3|y-z|+|y|^3|z-x|+|z|^3|x-y|\ge |x-y||y-z||z-x||x+y+z|.\)

It is easy to check the following identity:

\(\displaystyle x^3(y-z)+y^3(z-x)+z^3(x-y)=-(x-y)(y-z)(z-x)(x+y+z).\)

Let's apply the triangle inequlaity:

\(\displaystyle |x^3(y-z)|+|y^3(z-x)|+|z^3(x-y)|\ge |(x-y)(y-z)(z-x)(x+y+z)|.\)

Using identity \(\displaystyle |uv|=|u||v|\) several times we get what we had to prove:

\(\displaystyle |x|^3|y-z|+|y|^3|z-x|+|z|^3|x-y|\ge |x-y||y-z||z-x||x+y+z|.\)

Statistics:

8 students sent a solution.
6 points:	Balogh Ádám Péter.
5 points:	1 student.
2 points:	2 students.
1 point:	4 students.

Problems in Mathematics of KöMaL, November 2021