 |
Az A. 817. feladat (2022. január) |
A. 817. Legyen \(\displaystyle ABC\) egy tetszőleges háromszög. Tekintsük azt a kört, amely érinti az \(\displaystyle AB\) és \(\displaystyle AC\) oldalt, és belülről érinti a háromszög körülírt körét a \(\displaystyle T\) pontban. A háromszög beírt körének középpontja legyen \(\displaystyle I\), és a beírt kör érintse a \(\displaystyle BC\), \(\displaystyle CA\), illetve \(\displaystyle AB\) oldalt a \(\displaystyle D\), \(\displaystyle E\), illetve \(\displaystyle F\) pontban. Legyen \(\displaystyle N\) a \(\displaystyle DF\) szakasz felezőpontja. Bizonyítsuk be, hogy a \(\displaystyle BTN\) háromszög körülírt köre, a \(\displaystyle TI\) egyenes és a \(\displaystyle D\) pontból az \(\displaystyle EF\) szakaszra állított merőleges egy ponton megy át.
Javasolta: Diaconescu Tashi (Románia)
(7 pont)
A beküldési határidő 2022. február 10-én LEJÁRT.
Megoldás. Először kimondunk néhány ismert lemmát amire szükségünk lesz. A teljesség kedvéért a bizonyításukat is leírjuk.
1. Lemma: Adott egy \(\displaystyle ABC\) háromszög. A \(\displaystyle D\) pont az \(\displaystyle ABC\) köréírt köréhez \(\displaystyle B\)-ben és \(\displaystyle C\)-ben húzott érintők metszéspontja. Ekkor \(\displaystyle AD\) szimmedián, azaz ha az \(\displaystyle AD\) egyenest tükrözzük az \(\displaystyle ABC\) háromszög \(\displaystyle A\)-ból induló belső szögfelezőjére, akkor az \(\displaystyle A\)-ból induló súlyvonal egyenesét kapjuk.
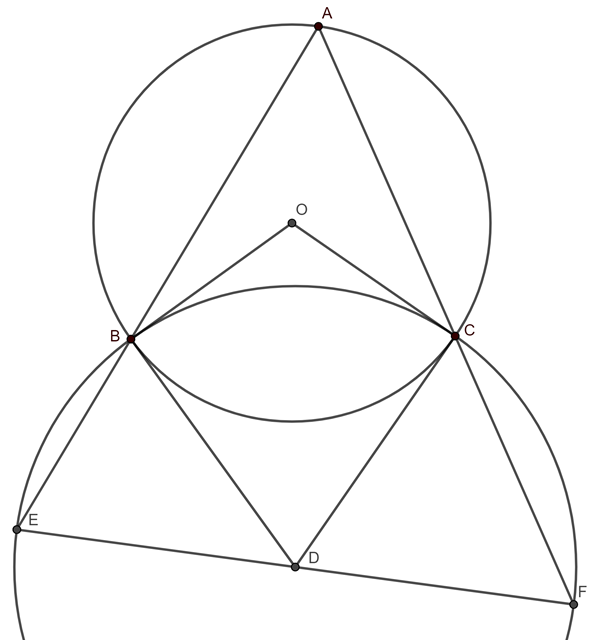
Bizonyítás: Vegyük fel a \(\displaystyle D\) középpontú, \(\displaystyle DB\) sugarú kört, ezt messe az \(\displaystyle AB\) és \(\displaystyle AC\) egyenes másodszor rendre az \(\displaystyle E\) és \(\displaystyle F\) pontokban. Legyen \(\displaystyle O\) az \(\displaystyle ABC\) köréírt körének középpontja. A \(\displaystyle D\) pont definíciója miatt \(\displaystyle OCD \sphericalangle=DBO \sphericalangle=90^{\circ}\), így \(\displaystyle BOC \sphericalangle+CDB \sphericalangle=180^{\circ}\). A kerületi és középponti szögek tételét használva
\(\displaystyle EBF \sphericalangle=BAF\sphericalangle+AFB\sphericalangle=\frac{1}{2}(BOC\sphericalangle+CDB\sphericalangle)=90^{\circ},\)
Így \(\displaystyle EF\) átmérő a \(\displaystyle D\) középpontú körben, tehát \(\displaystyle D\) az \(\displaystyle EF\) szakasz felezőpontja. \(\displaystyle EBCF\) húrnégyszög, így \(\displaystyle ABC\) és \(\displaystyle AFE\) hasonló háromszögek. Emiatt ha az \(\displaystyle ABC\) háromszög \(\displaystyle A\)-ból induló súlyvonalát tükrözzük a szögfelezőre, akkor pont az \(\displaystyle AFE\) súlyvonalát, az \(\displaystyle AD\) egyenest kapjuk, és ezt akartuk bizonyítani.
2. Lemma: Legyen \(\displaystyle ABC\) háromszög, legyenek \(\displaystyle D\), \(\displaystyle E\) és \(\displaystyle F\) rendre a szemközti csúcsot nem tartalmazó \(\displaystyle BC\), \(\displaystyle AC\) és \(\displaystyle AB\) ív felezőpontjai a háromszög köréírt körén. Ekkor \(\displaystyle EF\) merőleges \(\displaystyle AD\) szögfelezőre. Továbbá az \(\displaystyle ABC\) háromszög beírt körének középpontja megegyezik a \(\displaystyle DEF\) háromszög magasságpontjával.
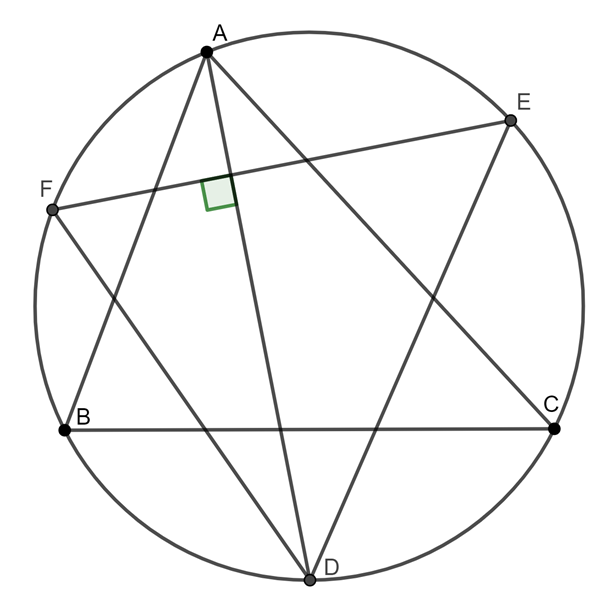
Bizonyítás: A szögekre a szokásos jelölést használva \(\displaystyle EFA \sphericalangle=\beta/2\) és \(\displaystyle FAD \sphericalangle=\alpha/2+\gamma/2\), így tényleg merőleges \(\displaystyle AD\) és \(\displaystyle EF\). Emiatt az \(\displaystyle AD\) egyenes egyben a \(\displaystyle BAC \sphericalangle\) szögfelezője és a \(\displaystyle D\)-ből induló magasságvonal a \(\displaystyle DEF\) háromszögben, amiből a lemma állítása következik.
3. Lemma: Legyen az \(\displaystyle ABC\) háromszög magasságpontja \(\displaystyle H\), köréírt körének középpontja \(\displaystyle O\). Jelölje a \(\displaystyle BC\) oldal felezőpontját \(\displaystyle F\), tovább legyen \(\displaystyle D\) az \(\displaystyle A\)-val átellenes pont a köréírt körön. Ekkor \(\displaystyle D\), \(\displaystyle F\) és \(\displaystyle H\) egy egyenesre esnek, ráadásul \(\displaystyle F\) a \(\displaystyle DH\) szakasz felezőpontja. Továbbá \(\displaystyle HA=2 \cdot FO\).
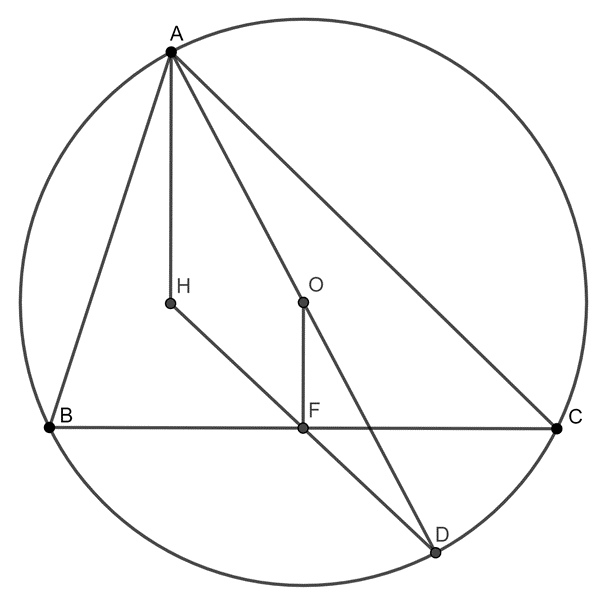
Bizonyítás: A lemma első fele egyszerű szögszámolás. Legyen \(\displaystyle D'\) a \(\displaystyle H\) tükörképe az \(\displaystyle F\) pontra. \(\displaystyle BHC \sphericalangle=180^{\circ}-\alpha\), és \(\displaystyle HBD'C\) paralelogramma, így a \(\displaystyle CD'B\sphericalangle\) is ennyi, azaz \(\displaystyle D'\) a köréírt körön helyezkedik el. Továbbá \(\displaystyle D'BA \sphericalangle=CBA\sphericalangle+HCB\sphericalangle=90^{\circ}\), így \(\displaystyle D'\) az \(\displaystyle A\)-val átellenes pont, azaz \(\displaystyle D'=D\). A \(\displaystyle DHA\) háromszögben \(\displaystyle FO\) középvonal, így \(\displaystyle HA=2 \cdot FO\), ezzel a lemma bizonyítását befejeztük.
4. Lemma: Legyen az \(\displaystyle ABC\) háromszög köréírt köre \(\displaystyle k\), és legyen \(\displaystyle c\) az a kör ami belülről érinti a \(\displaystyle k\) kört a \(\displaystyle T\) pontban, továbbá érinti az \(\displaystyle AB\) és \(\displaystyle AC\) oldalakat rendre a \(\displaystyle T_1\) és \(\displaystyle T_2\) pontokban. Legyen \(\displaystyle U\) az \(\displaystyle A\)-t tartalmazó \(\displaystyle BC\) ív felezőpontja a \(\displaystyle k\) körön. Jelölje \(\displaystyle I\) az \(\displaystyle ABC\) háromszög beírt körének a középpontját. Ekkor \(\displaystyle I\) a \(\displaystyle T_1T_2\) szakasz felezőpontja, továbbá a \(\displaystyle T\), \(\displaystyle I\) és \(\displaystyle U\) pontok egy egyenesre esnek.
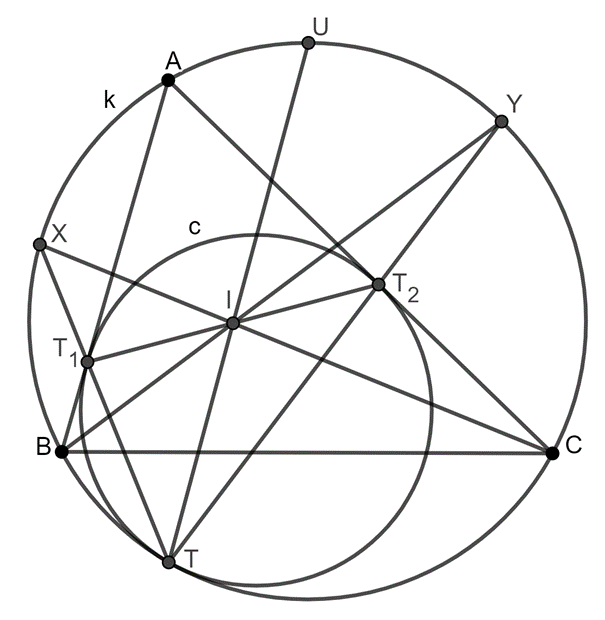
Bizonyítás: Legyen \(\displaystyle X\) és \(\displaystyle Y\) rendre a \(\displaystyle C\)-t és \(\displaystyle B\)-t nem tartalmazó \(\displaystyle AB\) és \(\displaystyle AC\) ív felezőpontja a \(\displaystyle k\) körön. Látható, hogy ha \(\displaystyle T\)-ből nagyítva a \(\displaystyle c\) kört a \(\displaystyle k\) körbe visszük, akkor \(\displaystyle T_1\) az \(\displaystyle X\) pontba, míg \(\displaystyle T_2\) az \(\displaystyle Y\) pontba megy, így \(\displaystyle T\), \(\displaystyle T_1\) és \(\displaystyle X\) valamint \(\displaystyle T\), \(\displaystyle T_2\) és \(\displaystyle Y\) egy egyenesre esik. Alkalmazzuk a Pascal-tételt a \(\displaystyle TXCABY\) (hurkolt) hatszögre. Ez pont azt adja, hogy \(\displaystyle T_1\), \(\displaystyle T_2\) és \(\displaystyle I\) egy egyenesre esnek. \(\displaystyle I\) rajta van az \(\displaystyle ABC\) háromszög \(\displaystyle A\)-ból induló szögfelezőjén, és \(\displaystyle AT_1T_2\) egyenlőszárú, mivel \(\displaystyle AT_1\) és \(\displaystyle AT_2\) érinti a \(\displaystyle c\) kört, így \(\displaystyle I\) tényleg a \(\displaystyle T_1T_2\) szakasz felezőpontja.
A 2. Lemma miatt \(\displaystyle XY\) párhuzamos az \(\displaystyle A\)-ból induló külső szögfelezővel, azaz \(\displaystyle AU\)-val, így \(\displaystyle XAUY\) húrtrapéz, tehát az \(\displaystyle XA\) és \(\displaystyle UY\) ívek ugyanolyan hosszúak. Emiatt \(\displaystyle YTU\sphericalangle=ATX\sphericalangle\) teljesül. Az 1. Lemma miatt \(\displaystyle TA\) szimmedián a \(\displaystyle TT_1T_2\) háromszögben, és bizonyítottuk, hogy \(\displaystyle TI\) súlyvonal, így \(\displaystyle ATT_1 \sphericalangle=T_2TI\sphericalangle\). Ezeket összevetve \(\displaystyle YTU \sphericalangle=YTI\sphericalangle\), ami pont azt jelenti, hogy \(\displaystyle T\), \(\displaystyle I\) és \(\displaystyle U\) egy egyenesre esnek.
Térjünk rá a feladat bizonyítására. Legyen \(\displaystyle k\) az \(\displaystyle ABC\) köréírt köre, és legyen \(\displaystyle d\) a beírt köre. Legyen \(\displaystyle f\) a pozitív arányú nagyítás, ami a \(\displaystyle k\) kört a \(\displaystyle d\)-be viszi. Legyen \(\displaystyle f(A)=A'\), \(\displaystyle f(B)=B'\) és \(\displaystyle f(C)=C'\). Legyen a \(\displaystyle k\) kör \(\displaystyle A\)-t tartalmzó \(\displaystyle BC\) ívének felezőpontja \(\displaystyle U\), a \(\displaystyle d\) kör \(\displaystyle A'\)-t tartalmzó \(\displaystyle B'C'\) ívének felezőpontja \(\displaystyle V\). Ekkor \(\displaystyle f(U)=V\). Legyen \(\displaystyle H\) a \(\displaystyle DEF\) háromszög magasságpontja. Jelölje továbbá \(\displaystyle Z\) a \(\displaystyle TI\) és \(\displaystyle DH\) egyenesek metszéspontját. Ekkor azt kell igazolnunk, hogy \(\displaystyle T\), \(\displaystyle Z\), \(\displaystyle N\) és \(\displaystyle B\) egy körre illeszkednek. Végül jelölje az \(\displaystyle EF\) és \(\displaystyle DE\) szakaszok felezőpontját rendre \(\displaystyle M\) és \(\displaystyle P\).
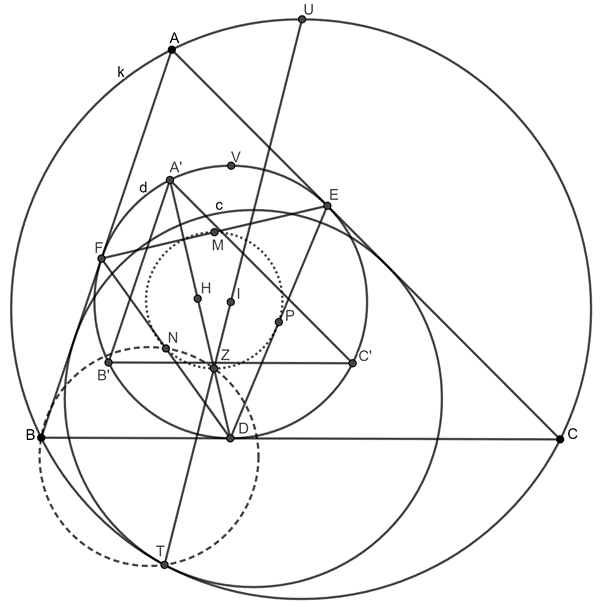
Világos, hogy a \(\displaystyle D\), \(\displaystyle E\) és \(\displaystyle F\) pontok rendre a \(\displaystyle B'C'\), \(\displaystyle A'C'\) és \(\displaystyle A'B'\) ívek felezőpontjai a \(\displaystyle d\) körön, így a 2. Lemma szerint \(\displaystyle H\) az \(\displaystyle A'B'C'\) háromszög beírt körének középpotja, így \(\displaystyle f(I)=H\). Ebből, és hogy \(\displaystyle f(U)=V\) következik, hogy az \(\displaystyle UI\) és \(\displaystyle HV\) egyenesek párhuzamosak. Látható, hogy \(\displaystyle V\) a \(\displaystyle D\) ponttal szemközti pont a \(\displaystyle d\) körön, így a 3. Lemmát alkalmazva a \(\displaystyle DEF\) háromszögben kapjuk, hogy \(\displaystyle H\), \(\displaystyle M\) és \(\displaystyle V\) egy egyenesre esnek. Továbbá a 4. Lemma miatt \(\displaystyle U\), \(\displaystyle I\), \(\displaystyle Z\) és \(\displaystyle T\) pontok is egy egyenesen vannak, így \(\displaystyle IZ\) és \(\displaystyle MH\) párhuzamosak. Vegyük észre, hogy \(\displaystyle ZH\) és \(\displaystyle IM\) is merőleges az \(\displaystyle EF\) egyenesre, azaz egymással párhuzamosak. Ezek alapján \(\displaystyle MHZI\) paralelogramma, tehát \(\displaystyle MI=HZ\). Alkalmazva a 3. Lemmát adódik, hogy \(\displaystyle 2 \cdot MI=HD\), így \(\displaystyle Z\) a \(\displaystyle HD\) szakasz felezőpontja. Ez azt jelenti, hogy \(\displaystyle Z\) rajta van a \(\displaystyle DEF\) háromszög Feuerbach-körén, amin \(\displaystyle N\), \(\displaystyle M\) és \(\displaystyle P\) is rajta van.
Jelölje \(\displaystyle g\) a \(\displaystyle d\) körre vonatkozó inverziót. Ismer és könnyű meggondolni, hogy \(\displaystyle g(M)=A\) (mivel az \(\displaystyle A\) pont polárisa a \(\displaystyle d\) körre nézve az \(\displaystyle EF\) egyenes), és hasonlóan \(\displaystyle g(P)=C\) és \(\displaystyle g(N)=B\). Tehát a \(\displaystyle g\) transzformáció a \(\displaystyle DEF\) háromszög Feuerbach-körét a \(\displaystyle k\) körbe viszi. Emiatt \(\displaystyle g(Z)=T\). Ebből azonban kész vagyunk, mert ismert tuljadonsága az inverziónak (és a pont körre vonatkozó hatványának megfordításából egyszerűen látszik), hogy \(\displaystyle NZg(Z)g(N)\), azaz \(\displaystyle NZTB\) húrnégyszöget alkot. Ezzel a feladat állítását bizonyítottuk.
Statisztika:
12 dolgozat érkezett. 7 pontot kapott: Bán-Szabó Áron, Diaconescu Tashi, Molnár-Szabó Vilmos, Seres-Szabó Márton, Varga Boldizsár. 6 pontot kapott: Ben Gillott, Nádor Benedek. 3 pontot kapott: 2 versenyző. 1 pontot kapott: 3 versenyző.
A KöMaL 2022. januári matematika feladatai

