 Problem A. 820. (February 2022)
Problem A. 820. (February 2022)
A. 820. Let \(\displaystyle ABC\) be an arbitrary triangle. Let the excircle tangent to side \(\displaystyle a\) be tangent to lines \(\displaystyle AB\), \(\displaystyle BC\) and \(\displaystyle CA\) at points \(\displaystyle C_a\), \(\displaystyle A_a\) and \(\displaystyle B_a\), respectively. Similarly, let the excircle tangent to side \(\displaystyle b\) be tangent to lines \(\displaystyle AB\), \(\displaystyle BC\) and \(\displaystyle CA\) at points \(\displaystyle B_c\), \(\displaystyle B_a\) and \(\displaystyle B_b\), respectively. Finally, let the excircle tangent to side \(\displaystyle c\) be tangent to lines \(\displaystyle AB\), \(\displaystyle BC\) and \(\displaystyle CA\) at points \(\displaystyle C_c\), \(\displaystyle A_c\) and \(\displaystyle B_c\), respectively. Let \(\displaystyle A'\) be the intersection of lines \(\displaystyle A_bC_b\) and \(\displaystyle A_cB_c\). Similarly, let \(\displaystyle B'\) be the intersection of lines \(\displaystyle B_aC_a\) and \(\displaystyle A_cB_c\), and let \(\displaystyle C'\) be the intersection of lines \(\displaystyle B_aC_a\) and \(\displaystyle A_bC_b\). Finally, let the incircle be tangent to sides \(\displaystyle a\), \(\displaystyle b\) and \(\displaystyle c\) at points \(\displaystyle T_a\), \(\displaystyle T_b\) and \(\displaystyle T_c\), respectively.
\(\displaystyle a)\) Prove that lines \(\displaystyle A'A_a\), \(\displaystyle B'B_b\) and \(\displaystyle C'C_c\) are concurrent.
\(\displaystyle b)\) Prove that lines \(\displaystyle A'T_a\) and \(\displaystyle B'T_b\) and \(\displaystyle C'T_c\) are also concurrent, and their point of intersection is on the line defined by the orthocentre and the incentre of triangle \(\displaystyle ABC\).
Submitted by Viktor Csaplár, Bátorkeszi and Dániel Hegedűs, Gyöngyös
(7 pont)
Deadline expired on March 10, 2022.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. a) Az állítást a trigonometrikus Ceva-tétellel fogjuk belátni. Az \(\displaystyle A_bA'A_a\sphericalangle\) szöget jelölje \(\displaystyle x\), az \(\displaystyle A_cA'A_a\sphericalangle\) szöget pedig \(\displaystyle y\). A \(\displaystyle \sin x/\sin y\) arányt az \(\displaystyle A'A_bA_c\) háromszög segítségével számoljuk ki. Ismert, hogy a szokásos jelölésekkel \(\displaystyle CA_b=s-a\), \(\displaystyle CA_a=s-b\), így \(\displaystyle A_bA_a=(s-a)+(s-b)=c\). Hasonlóan bizonyítható, hogy \(\displaystyle A_CA_a=b\). A szinusz-tételt alkalmazva az \(\displaystyle A'A_aA_b\) háromszögben (felhasználva, hogy \(\displaystyle A_aA_bC_b\sphericalangle=\frac{\pi-\beta}{2}\)) megkapjuk, hogy \(\displaystyle \frac{\sin x}{\sin \frac{\pi-\beta}{2}}=\frac{c}{A'A_a}\). Hasonlóan, a szinusz-tételt az \(\displaystyle A'A_aA_c\) háromszögben alkalmazva \(\displaystyle \frac{\sin y}{\sin \frac{\pi-\gamma}{2}}=\frac{b}{A'A_a}\). A két arány hányadosát véve \(\displaystyle \frac{\sin x}{\sin y}=\frac{c\cos \frac{\beta}{2}}{b\cos\frac{\gamma}{2}}\). Innen logikai szimmetria miatt könnyen számolható a másik két arány is, és egyszerűen ellenőrizhető, hogy a három arány szorzata 1.
Megjegyzés: A megoldás során azt is észre lehet venni, hogy a szinusztételt és a \(\displaystyle \sin \gamma=2\sin \frac{\gamma}{2}\cos \frac{\gamma}{2}\) azonosságot felhasználva
\(\displaystyle \frac{\sin x}{\sin y}=\frac{c\cos \frac{\beta}{2}}{b\cos\frac{\gamma}{2}}=\frac{\sin\frac{\gamma}{2}}{\sin\frac{\beta}{2}}. \)
Most azt is észrevéve, hogy \(\displaystyle A_bA'A_c\sphericalangle=\pi-(\pi-\beta)/2-(\pi-\gamma)/2=\beta/2+\gamma/2\) azonnal adódik, hogy \(\displaystyle x=\gamma/2\) és \(\displaystyle y=\beta/2\). Innen pedig (felhasználva, hogy \(\displaystyle A'B'C'\) szögei \(\displaystyle (\alpha+\beta)/2\), \(\displaystyle (\beta+\gamma)/2\) és \(\displaystyle (\gamma+\alpha)/2\)) könnyű látni, hogy a metszéspont az \(\displaystyle A'B'C'\) háromszög magasságpontja.
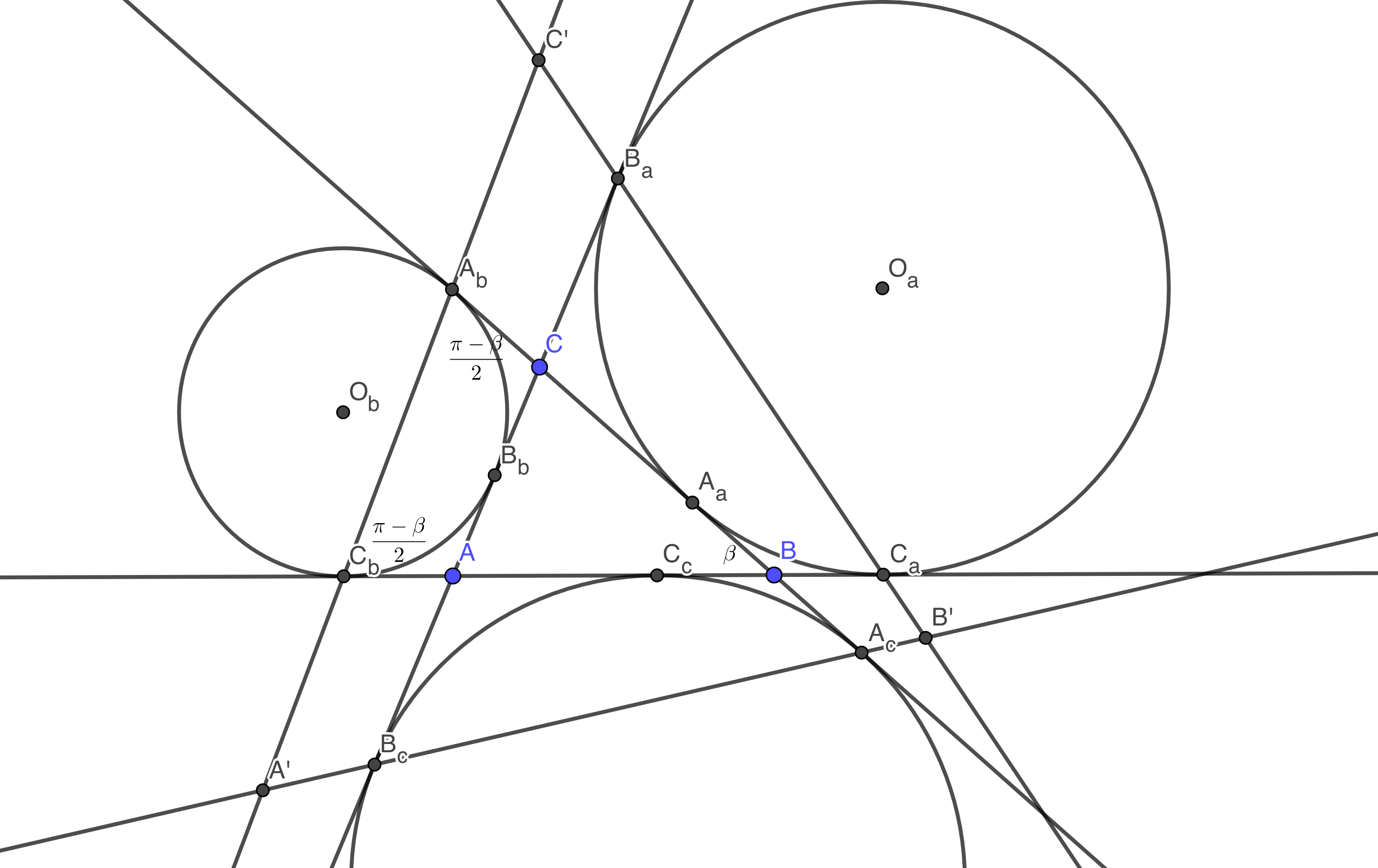
b) Először azt látjuk be, hogy \(\displaystyle A'A\) merőleges a \(\displaystyle BC\) oldalra. Ez úgy fog kijönni, hogy megmutatjuk, \(\displaystyle A'\) és \(\displaystyle A\) merőleges vetülete a \(\displaystyle BC\) oldalon ugyanaz a pont, pontosabban azt mutatjuk meg, hogy ugyanolyan arányban osztják a vetületek az \(\displaystyle A_bA_c\) szakaszt. Az \(\displaystyle A'\) merőleges vetülete (\(\displaystyle T'\)) könnyen látható, hogy \(\displaystyle A_bT'=A'T'\text{ctg}\frac{\pi-\beta}{2}=A'T'\text{tg}\frac{\beta}{2}\) és \(\displaystyle A_cT'=A'T'\text{ctg}\frac{\pi-\gamma}{2}=A'T'\text{tg}\frac{\gamma}{2}\) szakaszokra osztja \(\displaystyle A_bA_c\)-t. Az \(\displaystyle ABC\) háromszög \(\displaystyle A\)-ból induló magasságának talppontja (\(\displaystyle T\)) a \(\displaystyle BC\) oldalt jól ismert módon \(\displaystyle CT=\frac{a^2+b^2-c^2}{2a}\) és \(\displaystyle BT=\frac{a^2+c^2-b^2}{2a}\) hosszú szakaszokra bontja. Innen
\(\displaystyle A_bT=(s-a)+\frac{a^2+b^2-c^2}{2a}=\frac{(b+c-a)a+(a^2+b^2-c^2)}{2c}=\frac{(b+c)a+b^2-c^2}{2a}=\frac{(b+c)(a+b-c)}{2a}. \)
Hasonló módon
\(\displaystyle A_cT=(s-a)+\frac{a^2+c^2-b^2}{2a}=\frac{(b+c)(a+c-b)}{2a}. \)
Az osztóviszonyok egyenlőségéhez tehát azt kéne belátni, hogy
\(\displaystyle \frac{\text{tg}\frac{\beta}{2}}{\text{tg}\frac{\gamma}{2}}=\frac{a+b-c}{a+c-b}. \)
Ez pedig abból következik, hogy jól ismert és könnyen látható módon \(\displaystyle \text{tg}\frac{\beta}{2}(s-b)\) és \(\displaystyle \text{tg}\frac{\gamma}{2}(s-c)\) is megegyezik a beírt kör sugarával.
Ebből azonnal következik, hogy \(\displaystyle A'A\), \(\displaystyle B'B\) és \(\displaystyle C'C\) egy ponton mennek át, mégpedig az \(\displaystyle ABC\) háromszög magasságpontján.
A továbbiakhoz vegyük észre, hogy a bebizonyított merőlegesség miatt
\(\displaystyle C'A'A\sphericalangle=\pi/2-CA_bA'\sphericalangle=\pi/2-(\pi-\beta)/2=\beta/2 \)
és ugyanígy \(\displaystyle A'C'C\sphericalangle\) is \(\displaystyle \beta/2\). Így az \(\displaystyle A'C'\), \(\displaystyle A'A\) és \(\displaystyle C'C\) egyenesek egy egyenlő szárú háromszöget alkotnak, azaz \(\displaystyle A'A\) és \(\displaystyle C'C\) metszéspontja egyforma messze van \(\displaystyle A'\)-től és \(\displaystyle C'\)-től. Logikai szimmetria miatt tehát a metszéspont \(\displaystyle A'\)-től, \(\displaystyle B'\)-től és \(\displaystyle C'\)-től is egyforma messze van. Ezt azt jelenti, hogy \(\displaystyle AA'\), \(\displaystyle BB'\) és \(\displaystyle CC'\) metszéspontja (amellett, hogy az eredeti háromszög magasságpontja) az \(\displaystyle A'B'C'\) háromszög körülírt körének középpontja. Végül \(\displaystyle T_aT_c\) és \(\displaystyle A_bC_b\) párhuzamosak egymással, így \(\displaystyle A'B'C'\) és \(\displaystyle T_aT_bT_c\) középpontosan hasonlóak. A hasonlóság középpontja az \(\displaystyle A'T_a\), \(\displaystyle B'T_b\) és \(\displaystyle C'T_c\) egyenesek metszéspontja. Ennél a hasonlóságnál az \(\displaystyle A'B'C'\) körülírt köre középpontjának, azaz az \(\displaystyle ABC\) háromszög magasságpontjának képe a \(\displaystyle T_aT_bT_c\) háromszög körülírt körének középpontja, ami éppen az \(\displaystyle ABC\) háromszög beírt körének középpontja. Ezzel a b. rész állítását is beláttuk.
Statistics:
9 students sent a solution. 7 points: Ben Gillott, Chrobák Gergő, Diaconescu Tashi, Ho Tran Khanh Linh, Lovas Márton, Seres-Szabó Márton, Sztranyák Gabriella. 4 points: 1 student. 3 points: 1 student.
Problems in Mathematics of KöMaL, February 2022
