Problem A. 831. (September 2022)

A. 831. In triangle \(\displaystyle ABC\) let \(\displaystyle F\) denote the midpoint of side \(\displaystyle BC\). Let the circle passing through point \(\displaystyle A\) and tangent to side \(\displaystyle BC\) at point \(\displaystyle F\) intersect sides \(\displaystyle AB\) and \(\displaystyle AC\) at points \(\displaystyle M\) and \(\displaystyle N\), respectively. Let line segments \(\displaystyle CM\) and \(\displaystyle BN\) intersect in point \(\displaystyle X\). Let \(\displaystyle P\) be the second point of intersection of the circumcircles of triangles \(\displaystyle BMX\) and \(\displaystyle CNX\). Prove that points \(\displaystyle A\), \(\displaystyle F\) and \(\displaystyle P\) are collinear.

(7 pont)

Deadline expired on October 10, 2022.

Solution 1: Notice that \(\displaystyle P\) is the Miquel point of lines \(\displaystyle AMB\), \(\displaystyle ANC\), \(\displaystyle BXN\) and \(\displaystyle CXM\), so circles \(\displaystyle ABN\) and \(\displaystyle ACM\) pass through \(\displaystyle P\). Let line \(\displaystyle BC\) meet circles \(\displaystyle ACPM\) and \(\displaystyle ABPN\) at \(\displaystyle Q\) and \(\displaystyle R\), respectively.

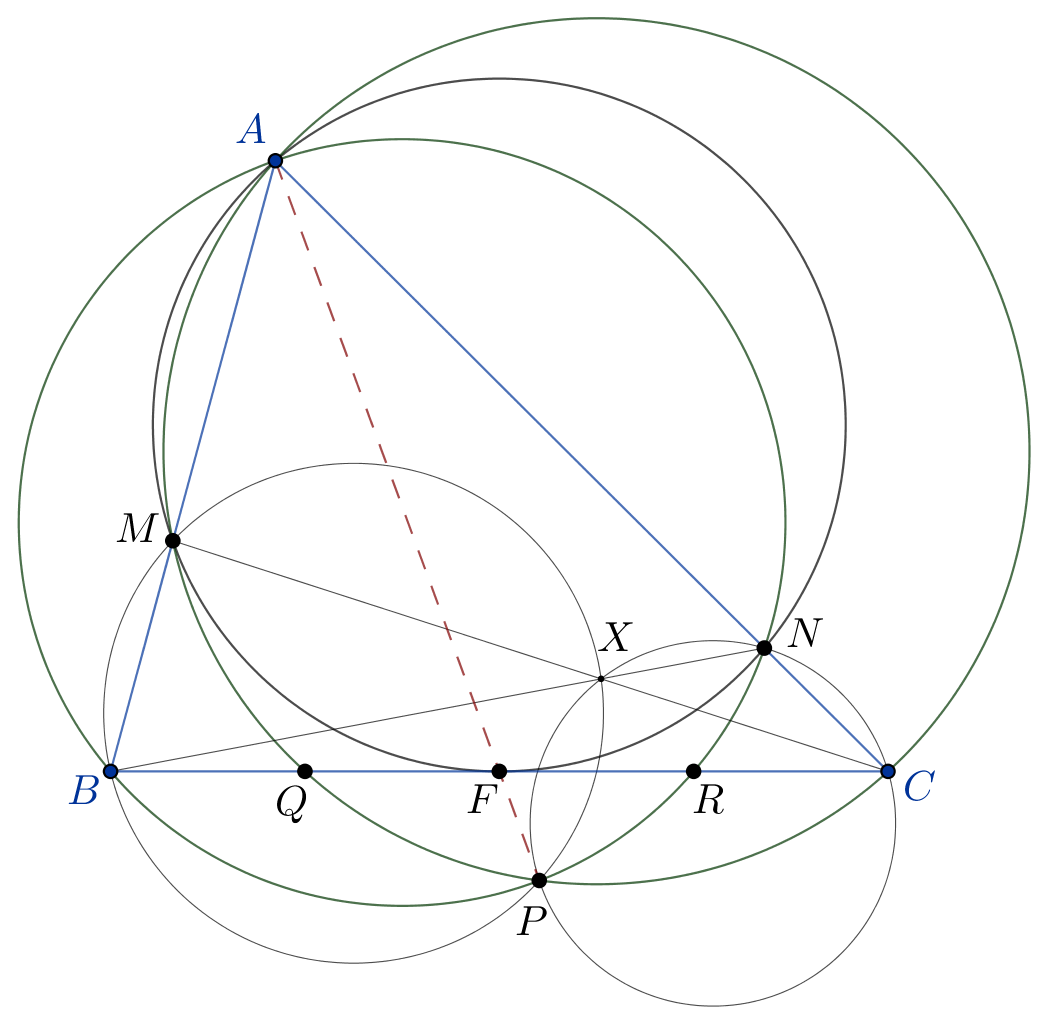
From the powers of point \(\displaystyle B\) with respect to circles \(\displaystyle ACPQM\) and \(\displaystyle AMFN\) we get

\(\displaystyle BQ\cdot BC = BA\cdot BM = AF^2 = \left(\dfrac{BC}2\right)^2, \)

hence \(\displaystyle BQ=\dfrac{BC}4\). Analogously, from the powers of \(\displaystyle C\) with recpect to circles \(\displaystyle ABPRN\) and \(\displaystyle AMFN\) we obtain \(\displaystyle RC=\dfrac{BC}4\).Therefore, \(\displaystyle Q\) and \(\displaystyle R\) are the quartering points of side \(\displaystyle BC\).

Finally, the powers of point \(\displaystyle F\) with respect to circles \(\displaystyle ABPRN\) and \(\displaystyle AMQPC\) are equal because

\(\displaystyle FB\cdot FR = \frac{-BC}2\cdot\frac{BC}4 = \frac{BC}2\cdot\frac{-BC}4 = FC\cdot FQ. \)

So, \(\displaystyle F\) lies on the radical axis of those two circles, that is line \(\displaystyle AP\).

Solution 2: Let \(\displaystyle d(X,e)\) denote the distance of point \(\displaystyle X\) and line \(\displaystyle e\). We will use the usual notation of \(\displaystyle a,b,c\) for the lengths of the sides of triangle \(\displaystyle ABC\). Using the power of point \(\displaystyle B\) for circle \(\displaystyle AMFN\), \(\displaystyle BM\cdot BA=BF^2\), thus \(\displaystyle BM=\frac{a^2}{4c}\). Similarly we get \(\displaystyle CN=\frac{a^2}{4b}\). Observe that triangles \(\displaystyle PCN\) and \(\displaystyle PMB\) are similar. This is a well known property of the composition of a rotation and dilation with the same center, but it's also easy with a little bit of angle chasing:

\(\displaystyle \angle MPB =\angle MXB = \angle CXN = \angle CPN,\)

and

\(\displaystyle \angle BMP = \angle BXP =180^{\circ}-\angle PXN = \angle NCP.\)

Thus the ratio of the heights from \(\displaystyle P\) to \(\displaystyle NC\) and \(\displaystyle MB\) is the same as the ratio of the similarity, i.e. \(\displaystyle \frac{d(P,AC)}{d(P,AB)}=\frac{CN}{MB}=\frac{c}{b}\).It is clear that the locus of points the distance (with sign) of which from \(\displaystyle AC\) and \(\displaystyle AB\) equals \(\displaystyle \frac{c}{b}\) is a line containing point \(\displaystyle A\), thus it is enough to verify that point \(\displaystyle F\) is also on this line. The area of triangles \(\displaystyle ABF\) and \(\displaystyle AFC\) is the same, let's denote it by \(\displaystyle T\), and so \(\displaystyle c \cdot d(F,AB)=2T=b \cdot d(F,AC)\), and this is exactly what we needed.

Statistics:

24 students sent a solution.
7 points:	Archit Manas, Arnab Sanyal, Bodor Mátyás, Bognár 171 András Károly, Chrobák Gergő, Diaconescu Tashi, Foris Dávid, Fülöp Csilla, Ho Tran Khanh Linh, Molnár-Szabó Vilmos, Móricz Benjámin, Németh Márton, Nguyen Kim Dorka, Seres-Szabó Márton, Sztranyák Gabriella, Tarján Bernát, Varga Boldizsár, Virág Rudolf, Wiener Anna.
6 points:	Lovas Márton, Nádor Benedek, Simon László Bence.
0 point:	2 students.

Problems in Mathematics of KöMaL, September 2022