Problem A. 834. (October 2022)

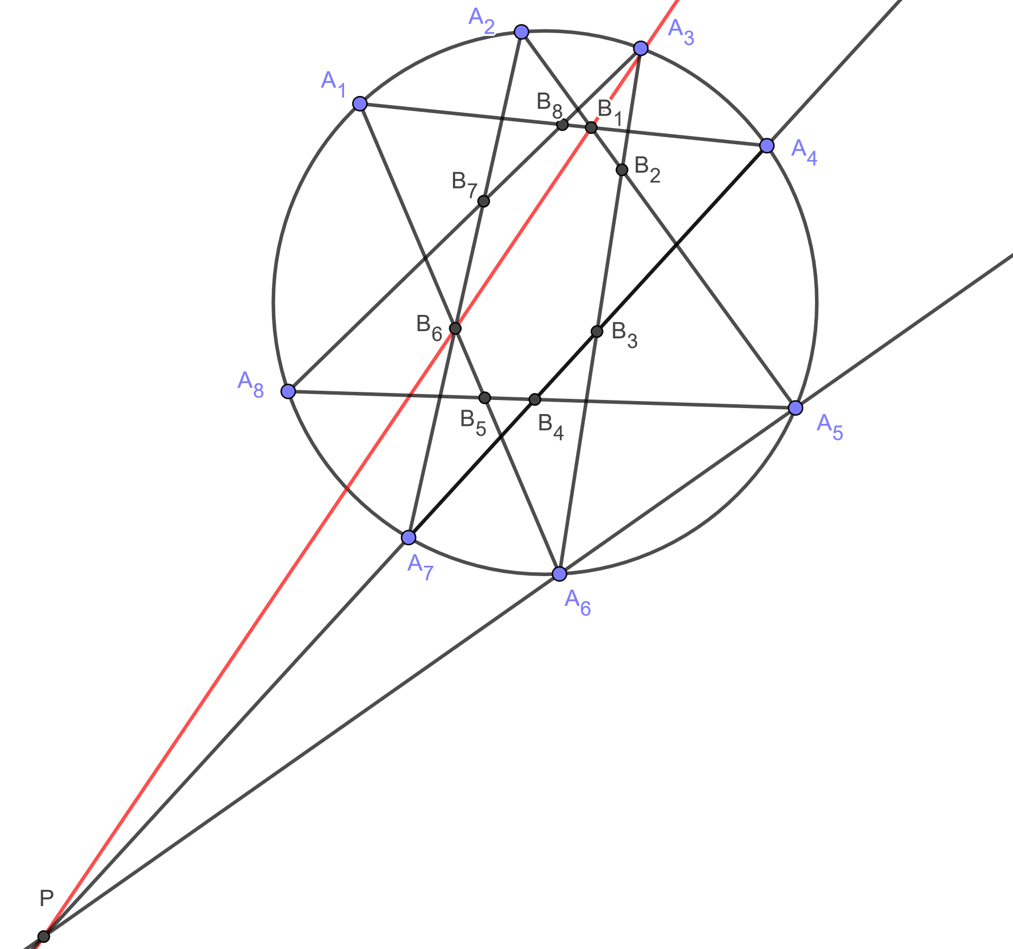
A. 834. Let \(\displaystyle A_1A_2\ldots A_8\) be a convex cyclic octagon, and for \(\displaystyle i=1,2\ldots,8\) let \(\displaystyle B_i=A_iA_{i+3}\cap A_{i+1}A_{i+4}\) (indices are meant modulo 8). Prove that points \(\displaystyle B_1,\ldots,B_8\) lie on the same conic section.

(7 pont)

Deadline expired on November 10, 2022.

Apply Pascal's theorem to the looped hexagon \(\displaystyle A_1A_6A_5A_2A_7A_4\). We have \(\displaystyle A_1A_6\cap A_2A_7=B_6\), \(\displaystyle A_6A_5\cap A_7A_4=P\) (this is the definition of the point \(\displaystyle P\)) and \(\displaystyle A_5A_2\cap A_4A_1=B_1\), so \(\displaystyle B_1\), \(\displaystyle B_6\) and \(\displaystyle P\) are collinear. Now consider the hexagon \(\displaystyle B_1B_2B_3B_4B_5B_6\). We have \(\displaystyle B_1B_2\cap B_4B_5=A_5\), \(\displaystyle B_2B_3\cap B_5B_6=A_6\), and finally, \(\displaystyle B_3B_4\cap B_6B_1=P\), because the line \(\displaystyle B_3B_4\) is equal to the line \(\displaystyle A_4A_7\), and contains the point \(\displaystyle P\) by definition of \(\displaystyle P\). Also by the definition of \(\displaystyle P\), points \(\displaystyle A_5\), \(\displaystyle A_6\) and \(\displaystyle P\) lie on a line, so by the converse of Pascal's theorem, \(\displaystyle B_1B_2B_3B_4B_5B_6\) falls on a conic section. Since 5 points determine a conic section, from here we are done by cyclic iteration of this.

Statistics:

16 students sent a solution.
7 points:	Chrobák Gergő, Diaconescu Tashi, Farkas 005 Bendegúz, Lovas Márton, Molnár-Szabó Vilmos, Móra Márton Barnabás, Nádor Benedek, Németh Márton, Seres-Szabó Márton, Simon László Bence, Sztranyák Gabriella, Tarján Bernát, Varga Boldizsár, Virág Rudolf, Wiener Anna.
5 points:	1 student.

Problems in Mathematics of KöMaL, October 2022