 |
Az A. 837. feladat (2022. november) |
A. 837. Az \(\displaystyle A_1A_2A_3A_4\) tetraéder minden éle érint egy \(\displaystyle G\) gömböt; az \(\displaystyle A_i\) csúcsból a \(\displaystyle G\)-hez húzott érintőszakasz hossza legyen \(\displaystyle a_i\). Mutassuk meg, hogy
\(\displaystyle \bigg(\sum_{i=1}^4 \frac 1{a_i}\bigg)^{\!\!2}> 2\bigg(\sum_{i=1}^4 \frac1{a_i^2}\bigg). \)
Javasolta: Vígh Viktor (Szeged)
(7 pont)
A beküldési határidő 2022. december 12-én LEJÁRT.
Fel fogjuk használni a híres Descartes 4-kör tételt, ami a következőt mondja: a síkon 4 körre pontosan akkor teljesül, hogy páronként kívülről érintik egymást (lásd ábra), ha az \(\displaystyle r_1, r_2, r_3\) és \(\displaystyle r_4\) sugaraikra fennáll az alábbi azonosság:
\(\displaystyle \left(\frac{1}{r_1}+\frac{1}{r_2}+\frac{1}{r_3}+\frac{1}{r_4}\right)^2=2\left(\frac{1}{r_1^2}+\frac{1}{r_2^2}+\frac{1}{r_3^2}+\frac{1}{r_4^2}\right).\)
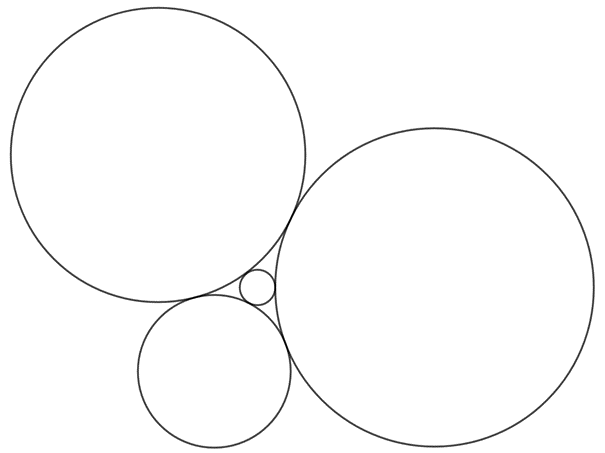
Ennek a tételnek itt nem részletezzük a bizonyítását. Meglepően nehéz a bizonyítása ahhoz képest, hogy mennyire egyszerű a konfiguráció, de számos bizonyítást lehet találni az interneten, kijön többek között a Hérón-képlet segítségével, trigonometriával vagy lineáris algebrai ötletekkel is.
Térjünk rá a feladatra. Legyen az \(\displaystyle A_i\) középpontú \(\displaystyle a_i\) sugarú gömb \(\displaystyle g_i\) minden \(\displaystyle 1 \leq i \leq 4\) esetén. Figyeljük meg, hogy a feltételek miatt ezek a gömbök páronként kívülről érintik egymást. Feltehetjük, hogy \(\displaystyle a_1 \geq a_2 \geq a_3 \geq a_4\). Vetítsük le ezeket a gömböket az \(\displaystyle A_1A_2A_3\) háromszög által meghatározott síkba. Legyen a vetítés után a \(\displaystyle g_i\) gömb képe a \(\displaystyle h_i\) kör (\(\displaystyle 1 \leq i \leq 4\)). Ez a sugarakon nem változtat, így a \(\displaystyle h_i\) kör sugara \(\displaystyle a_i\) (\(\displaystyle 1 \leq i \leq 4\)). Vizsgáljuk meg hogyan helyezkednek el egymáshoz képest ezek a körök. Egyrészt, a \(\displaystyle h_1\), \(\displaystyle h_2\) és \(\displaystyle h_3\) körök páronként kívülről érintik egymást, mivel érintő gömböket vetítettünk a középpontjaik által meghatározott síkra. Továbbá \(\displaystyle h_4\)-nek mind a három másik körrel kell lennie közös pontjának, mivel a vetítés előtt volt közös pontjuk a gömböknek (az érintési pont). Ráadásul az nem lehet, hogy \(\displaystyle h_4\) mind a három másik kört kívülről érinti, mivel az csak úgy lehetne, ha a gömböknek is ugyanezek lennének az érintési pontjaik, ám ekkor \(\displaystyle A_4\)-nek is az \(\displaystyle A_1A_2A_3\) síkba kéne esnie.
Legyen \(\displaystyle k_i=\frac{1}{a_i}\) minden \(\displaystyle 1 \leq i \leq 4\)-re, ekkor \(\displaystyle k_1 \leq k_2 \leq k_3 \leq k_4\). A feladat állítása ezekkel a jelölésekkel az, hogy
\(\displaystyle 2(k_1^2+k_2^2+k_3^2+k_4^2)<(k_1+k_2+k_3+k_4)^2.\)
Rendezzük ezt \(\displaystyle k_4\)-re:
\(\displaystyle 0<-k_4^2+2k_4(k_1+k_2+k_3)+((k_1+k_2+k_3)^2-2(k_1^2+k_2^2+k_3^2)).\)
Ez \(\displaystyle k_4\)-ben egy negatív főegyütthatójú másodfokú polinom, melynek \(\displaystyle x_1, x_2\) gyökeire teljesül, hogy
\(\displaystyle x_1+x_2=2(k_1+k_2+k_3)\)
és
\(\displaystyle x_1x_2=2(k_1^2+k_2^2+k_3^2)-(k_1+k_2+k_3)^2=(k_1+k_2+k_3)^2-4(k_1k_2+k_1k_3+k_2k_3).\)
Ebből könnyen adódik, hogy a két gyök éppen
\(\displaystyle x_{1,2}=k_1+k_2+k_3 \pm 2\sqrt{k_1k_2+k_1k_3+k_2k_3}.\)
Így a bizonyítandó állítás azzal ekvivalens, hogy \(\displaystyle x_1<k_4<x_2\).
Legyen \(\displaystyle h\) az a legkisebb sugarú kör, amelynek a \(\displaystyle h_1, h_2\) és \(\displaystyle h_3\) körökkel is van közös pontja. Világos, hogy ez egy értelmes definíció, létezik ilyen kör, méghozzá az, ami a \(\displaystyle h_1\), \(\displaystyle h_2\) és \(\displaystyle h_3\) körök által közrezárt régióban van, és mind a három kört érinti (kívülről). Ekkor a Descartes-tétel szerint
\(\displaystyle k=k_1+k_2+k_3+ 2\sqrt{k_1k_2+k_1k_3+k_2k_3},\)
ahol \(\displaystyle k\) a \(\displaystyle h\) kör sugarának reciproka. Mivel a \(\displaystyle h_4\) körnek a \(\displaystyle h_1\), \(\displaystyle h_2\) és \(\displaystyle h_3\) körökkel is van közös pontja, továbbá nem érinti mindhármat, ezért \(\displaystyle k_4<k=x_2\).
Már csak azt kell igazolni, hogy \(\displaystyle x_1<k_4\), azaz
\(\displaystyle k_1+k_2+k_3- 2\sqrt{k_1k_2+k_1k_3+k_2k_3}<k_4.\)
Ennél azt az erősebb állítást igazoljuk, hogy
\(\displaystyle k_1+k_2+k_3- 2\sqrt{k_1k_2+k_1k_3+k_2k_3}<k_3.\)
Ez pedig rendezve, majd négyzetre emelve azzal ekvivalens, hogy
\(\displaystyle k_1^2+2k_1k_2+k^2<4(k_1k_2+k_1k_3+k_2k_3),\)
ami valóban teljesül, mivel \(\displaystyle k_1 \leq k_2 \leq k_3\), így \(\displaystyle 2k_1k_2<4k_1k_2\), \(\displaystyle k_1^2<4k_1k_3\) és \(\displaystyle k_2^2<4k_2k_3\). Ezzel a bizonyítást befejeztük.
Statisztika:
9 dolgozat érkezett. 7 pontot kapott: Diaconescu Tashi, Lovas Márton, Nádor Benedek, Seres-Szabó Márton, Sztranyák Gabriella, Wiener Anna. 5 pontot kapott: 1 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2022. novemberi matematika feladatai

