Problem A. 837. (November 2022)

A. 837. Let all the edges of tetrahedron \(\displaystyle A_1A_2A_3A_4\) be tangent to sphere \(\displaystyle S\). Let \(\displaystyle a_i\) denote the length of the tangent from \(\displaystyle A_i\) to \(\displaystyle S\). Prove that

\(\displaystyle \bigg(\sum_{i=1}^4 \frac 1{a_i}\bigg)^{\!\!2}> 2\bigg(\sum_{i=1}^4 \frac1{a_i^2}\bigg). \)

Submitted by Viktor Vígh, Szeged

(7 pont)

Deadline expired on December 12, 2022.

We will use Descartes' theorem: the radii of every four mutually tangent circles satisfy the following:

\(\displaystyle \left(\frac{1}{r_1}+\frac{1}{r_2}+\frac{1}{r_3}+\frac{1}{r_4}\right)^2=2\left(\frac{1}{r_1^2}+\frac{1}{r_2^2}+\frac{1}{r_3^2}+\frac{1}{r_4^2}\right).\)

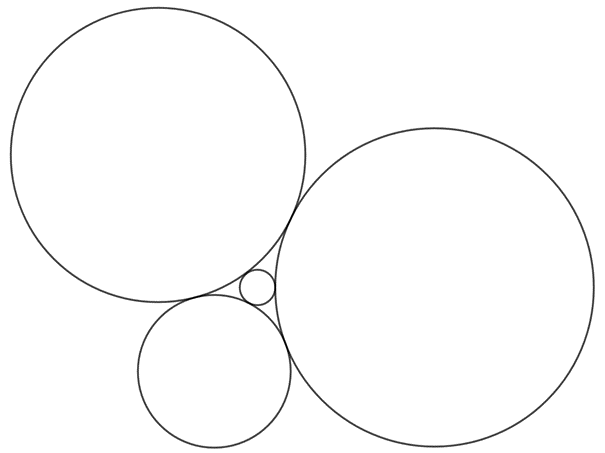
Let \(\displaystyle S_i\) denote the sphere with center \(\displaystyle A_i\) and radius \(\displaystyle a_i\). Note that these spheres are mutually tangent to each other. Without loss of generality we can assume that \(\displaystyle a_1 \geq a_2 \geq a_3 \geq a_4\). Let's project these spheres orthogonally onto the plane of triangle \(\displaystyle A_1A_2A_3\). Let \(\displaystyle C_i\) denote the projection of \(\displaystyle S_i\) (which is a circle). The radii of these circles are equal to the radii of the spheres. Circles \(\displaystyle C_1\), \(\displaystyle C_2\) and \(\displaystyle C_3\) are still mutually externally tangent to each other, because we projected them onto the plane of their centers. \(\displaystyle C_4\) has to has a common point with all three circles. Also, it is not possible that \(\displaystyle C_4\) is tangent to all three circles, since the spheres would have to have the same points of tangency, but then \(\displaystyle A_4\) would have to be in the plane of the other three points.

Let \(\displaystyle k_i=\frac{1}{a_i}\) for \(\displaystyle 1 \leq i \leq 4\). Then \(\displaystyle k_1 \leq k_2 \leq k_3 \leq k_4\). Using these notations the claim we have to prove becomes

\(\displaystyle 2(k_1^2+k_2^2+k_3^2+k_4^2)<(k_1+k_2+k_3+k_4)^2.\)

Let us rearrange it for \(\displaystyle k_4\):

\(\displaystyle 0<-k_4^2+2k_4(k_1+k_2+k_3)+((k_1+k_2+k_3)^2-2(k_1^2+k_2^2+k_3^2)).\)

This is a quadratic equation for \(\displaystyle k_4\) the roots of which are

\(\displaystyle x_{1,2}=k_1+k_2+k_3 \pm 2\sqrt{k_1k_2+k_1k_3+k_2k_3}.\)

Thus we have to prove that \(\displaystyle x_1<k_4<x_2\).

Let \(\displaystyle C\) be the circle of smallest radius that has a point in common with circles \(\displaystyle C_1, C_2\) and \(\displaystyle C_3\). Clearly, this is a reasonable definition, there exists such a circle, namely the one which is in the region bounded by the circles \(\displaystyle C_1\), \(\displaystyle C_2\) and \(\displaystyle C_3\) and which touches all three circles (from the outside). Then, by Descartes' theorem

\(\displaystyle k=k_1+k_2+k_3+ 2\sqrt{k_1k_2+k_1k_3+k_2k_3},\)

where \(\displaystyle k\) is the reciprocal of the radius of the circle \(\displaystyle C\). Since the circle \(\displaystyle C_4\) has a point in common with the circles \(\displaystyle C_1\), \(\displaystyle C_2\) and \(\displaystyle C_3\), and does not touch all three, \(\displaystyle k_4<k=x_2\).

It remains only to prove that \(\displaystyle x_1<k_4\), i.e.

\(\displaystyle k_1+k_2+k_3- 2\sqrt{k_1k_2+k_1k_3+k_2k_3}<k_4.\)

We prove the stronger claim

\(\displaystyle k_1+k_2+k_3- 2\sqrt{k_1k_2+k_1k_3+k_2k_3}<k_3.\)

This is equivalent to

\(\displaystyle k_1^2+2k_1k_2+k^2<4(k_1k_2+k_1k_3+k_2k_3),\)

which is indeed satisfied, since \(\displaystyle k_1 \leq k_2 \leq k_3\), so \(\displaystyle 2k_1k_2<4k_1k_2\), \(\displaystyle k_1^2<4k_1k_3\) and \(\displaystyle k_2^2<4k_2k_3\). This completes the proof.

Statistics:

9 students sent a solution.
7 points:	Diaconescu Tashi, Lovas Márton, Nádor Benedek, Seres-Szabó Márton, Sztranyák Gabriella, Wiener Anna.
5 points:	1 student.
1 point:	1 student.
0 point:	1 student.

Problems in Mathematics of KöMaL, November 2022