Problem A. 840. (December 2022)

A. 840. The incircle of triangle \(\displaystyle ABC\) touches the sides in \(\displaystyle X\), \(\displaystyle Y\) and \(\displaystyle Z\). In triangle \(\displaystyle XYZ\) the feet of the altitude from \(\displaystyle X\) and \(\displaystyle Y\) are \(\displaystyle X'\) and \(\displaystyle Y'\), respectively. Let line \(\displaystyle X'Y'\) intersect the circumcircle of triangle \(\displaystyle ABC\) at \(\displaystyle P\) and \(\displaystyle Q\). Prove that points \(\displaystyle X\), \(\displaystyle Y\), \(\displaystyle P\) and \(\displaystyle Q\) are concyclic.

Proposed by László Simon, Budapest

(7 pont)

Deadline expired on January 10, 2023.

Let \(\displaystyle D\) be the intersection of \(\displaystyle XY\) and \(\displaystyle X'Y'\). Since \(\displaystyle X\), \(\displaystyle Y\), \(\displaystyle X'\) and \(\displaystyle Y'\) are concylic, thus \(\displaystyle DX\cdot DY=DX'\cdot DY'\). So the power of point \(\displaystyle D\) with respect to the circumcircle and nine point circle of triangle \(\displaystyle XYZ\) is the same, thus it is on the radical axis of the two circles. We will show that the circumcircle of the original triangle is coaxial (they have the same radical axis) with these two circles. This will complete the argument, since the power of point \(\displaystyle D\) with respect to the circumcircle of triangle \(\displaystyle ABC\) is \(\displaystyle DP\cdot DQ\), thus \(\displaystyle DX\cdot DY=DP\cdot DQ\), so \(\displaystyle X\), \(\displaystyle Y\), \(\displaystyle P\) and \(\displaystyle Q\) are concyclic.

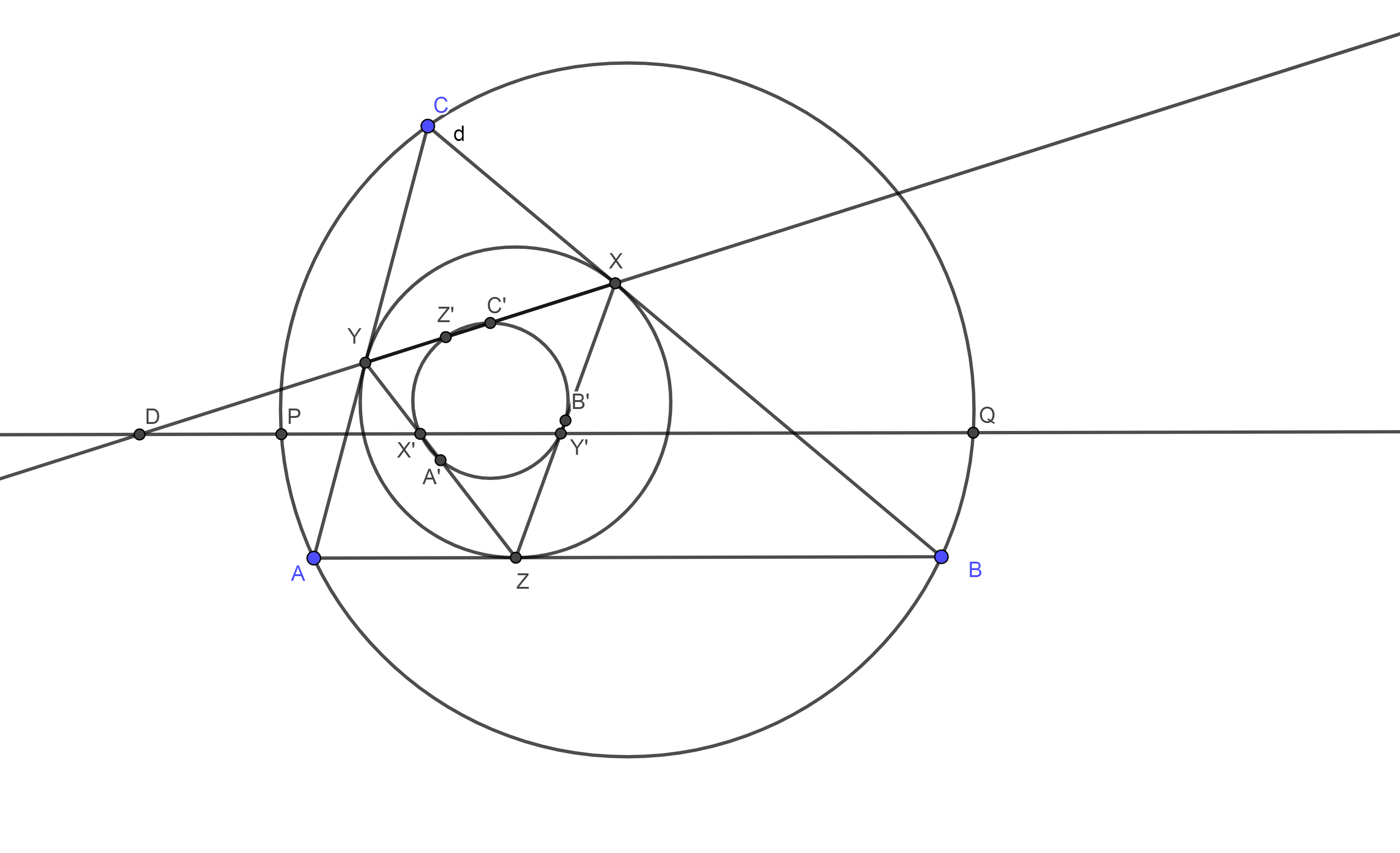
First we will show that the nine point circle of triangle \(\displaystyle XYZ\) is the inverse of the circumcircle of triangle \(\displaystyle ABC\) with respect to the circumcircle of triangle \(\displaystyle XYZ\). This is an immediate consequence of the following well known statement: the inverse image of an external point can be obtained by drawing tangents from the point to the circle of the inversion, and finding the midpoint of the two point of tangencies. Thus the inverse of point \(\displaystyle A\) is the midpoint of line segment \(\displaystyle YZ\), which is on the nine point circle of triangle \(\displaystyle XYZ\) and we get a similar argument also for points \(\displaystyle B\) and \(\displaystyle C\).

Finally we have to show the the circle of an inversion and two circles which are the inverses of each other are coaxial (let's denote these circles by \(\displaystyle c\), \(\displaystyle d\) and \(\displaystyle d'\)). This is obvious, if the two circle intersect each other, but unfortunately this is not the case here. Not that since the centers of the three circles are collinear, it is enough to find one point that has the same power with respect to all three circles.

In the general case do the following: find a circle (denote it by \(\displaystyle \gamma\)) that is perpendicular to circles \(\displaystyle c\) and \(\displaystyle d\). The inverse image of \(\displaystyle \gamma\) is itself (this is a well known property of the inversion), and since inversion is preserving angles, it also has to be perpendicular to the image of circle \(\displaystyle d\), which is circle \(\displaystyle d'\). Thus \(\displaystyle \gamma\) is perpendicular to all three circles, and so the power of its center is the same (the square of its radius) with respect to circles \(\displaystyle c\), \(\displaystyle d\) and \(\displaystyle d'\), and this finishes our proof.

Statistics:

20 students sent a solution.
7 points:	Diaconescu Tashi, Foris Dávid, Lovas Márton, Molnár-Szabó Vilmos, Móricz Benjámin, Németh Márton, Seres-Szabó Márton, Sida Li, Simon László Bence, Sztranyák Gabriella, Tarján Bernát, Varga Boldizsár, Virág Rudolf, Wiener Anna.
6 points:	Chrobák Gergő.
2 points:	2 students.
1 point:	2 students.
0 point:	1 student.

Problems in Mathematics of KöMaL, December 2022