Problem A. 844. (January 2023)

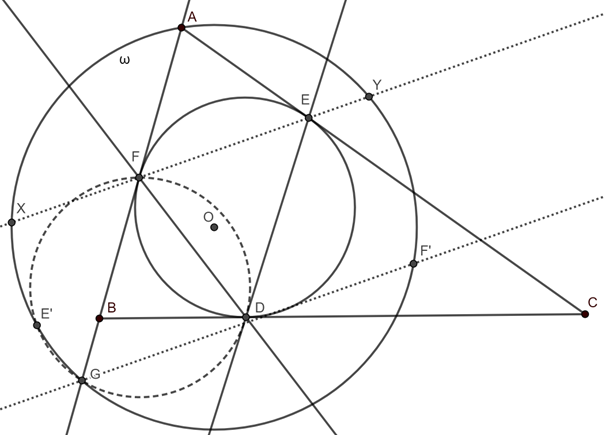
A. 844. The inscribed circle of triangle \(\displaystyle ABC\) is tangent to sides \(\displaystyle BC\), \(\displaystyle AC\) and \(\displaystyle AB\) at points \(\displaystyle D\), \(\displaystyle E\) and \(\displaystyle F\), respectively. Let \(\displaystyle E'\) be the reflection of point \(\displaystyle E\) across line \(\displaystyle DF\), and \(\displaystyle F'\) be the reflection of point \(\displaystyle F\) across line \(\displaystyle DE\). Let line \(\displaystyle EF\) intersect the circumcircle of triangle \(\displaystyle AE'F'\) at points \(\displaystyle X\) and \(\displaystyle Y\). Prove that \(\displaystyle DX=DY\).

Proposed by Márton Lovas, Budapest

(7 pont)

Deadline expired on February 10, 2023.

Without losing generality, let's assume \(\displaystyle AB < AC\). Let \(\displaystyle \omega\) be the circumcircle of \(\displaystyle AE'F'\) and let the line \(\displaystyle AB\) intersect \(\displaystyle \omega\) at point \(\displaystyle G \neq A\). We use the standard \(\displaystyle \alpha\), \(\displaystyle \beta\) and \(\displaystyle \gamma\) notations for the angles of the triangle \(\displaystyle ABC\).

Lemma 1 The triangles \(\displaystyle AEF'\) and \(\displaystyle AFE'\) are congruent.

Proof: Due to reflections, \(\displaystyle E'F=FE=EF'\), and \(\displaystyle AE=AF\). By angle calculations, we get

\(\displaystyle AEF' \angle=AEF \angle+FEF' \angle+DEF' \angle=\left(90^{\circ}-\frac{\alpha}{2}\right)+\left(90^{\circ}-\frac{\beta}{2}\right)+\left(90^{\circ}-\frac{\beta}{2}\right)=270^{\circ}-\frac{\alpha}{2}-\beta,\)

and

\(\displaystyle AFE' \angle=360^{\circ}-AFE \angle-EFD \angle-DEF' \angle=360^{\circ}-\left(90^{\circ}-\frac{\alpha}{2}\right)-\left(90^{\circ}-\frac{\gamma}{2}\right)-\left(90^{\circ}-\frac{\gamma}{2}\right)=\)

\(\displaystyle =270^{\circ}+\frac{\alpha}{2}+\gamma-180^{\circ}=270^{\circ}+\frac{\alpha}{2}+\gamma-(\alpha+\beta+\gamma)=270^{\circ}-\frac{\alpha}{2}-\beta,\)

so two sides and the angle between them are equal in these triangles, thus the lemma is proven. It is clear from this that the triangles \(\displaystyle AEF\) and \(\displaystyle AF'E'\) are similar.

Lemma 2 The quadrilateral \(\displaystyle FE'GD\) is a cyclic quadrilateral.

Proof: Note that

\(\displaystyle FGE' \angle=AGE' \angle=AF'E' \angle=AEF \angle=90^{\circ}-\frac{\alpha}{2}=FDE \angle=FDE',\)

from which the lemma follows.

Lemma 3 Point \(\displaystyle D\) is the center of the circumcircle of triangle \(\displaystyle FGF'\).

Proof: Observe that \(\displaystyle FGD \angle=FDE' \angle=\) \(\displaystyle FED \angle=90^{\circ}-\frac{\beta}{2}\), and \(\displaystyle GFD \angle=BFD \angle=90^{\circ}-\frac{\beta}{2}\), thus the triangle \(\displaystyle FDG\) is isosceles, i.e. \(\displaystyle FD=DG\). Furthermore, due to reflection, \(\displaystyle FD=DF'\), which completes the proof of the lemma.

Lemma 4 The lines \(\displaystyle GF'\) and \(\displaystyle EF\) are parallel.

Proof: Since \(\displaystyle A G F' \sphericalangle=A E' F' \sphericalangle=A F E \sphericalangle\), the two lines under examination enclose the same angle with line \(\displaystyle AB\), from which the statement of the lemma follows.

With these lemmas in hand, we can proceed to the task. Let \(\displaystyle O\) be the center of \(\displaystyle \omega\). A line connecting two points of intersection of two circles is perpendicular to the line connecting their centers, so \(\displaystyle O D\) is perpendicular to the line \(\displaystyle G F'\). Hence \(\displaystyle O D\) is also perpendicular to the line \(\displaystyle E F\), and \(\displaystyle OX=OY\), which means that \(\displaystyle O D\) is the perpendicular bisector of segment \(\displaystyle XY\), which proves the statement of the problem.

Statistics:

17 students sent a solution.
7 points:	Diaconescu Tashi, Elekes Dorottya, Foris Dávid, Lovas Márton, Molnár-Szabó Vilmos, Nádor Benedek, Németh Márton, Seres-Szabó Márton, Sida Li, Simon László Bence, Sztranyák Gabriella, Varga Boldizsár, Virág Rudolf, Wiener Anna.
4 points:	1 student.
2 points:	1 student.
Unfair, not evaluated:	1 solutions.

Problems in Mathematics of KöMaL, January 2023