 Problem A. 850. (March 2023)
Problem A. 850. (March 2023)
A. 850. Prove that there exists a positive real number \(\displaystyle N\) such that for arbitrary real numbers \(\displaystyle a,b>N\) it is possible to cover the perimeter of a rectangle with side lengths \(\displaystyle a\) and \(\displaystyle b\) using non-overlapping unit disks (the unit disks can be tangent to each other).
Submitted by Benedek Váli, Budapest
(7 pont)
Deadline expired on April 11, 2023.
First solution:
Choose \(\displaystyle N\) such that if \(\displaystyle a>N\), then \(\displaystyle \frac{a}{a+4} \geq \sqrt{1-1/100}\). We can do this, since \(\displaystyle \frac{a}{a+4} \to 1\) as \(\displaystyle a \to \infty\). This may seem quite random at this point, but we'll see in the solution why we chose \(\displaystyle N\) this way.
Let \(\displaystyle a,b>N\) be real numbers, and let the vertices of the rectangle be the points \(\displaystyle (0,0)\), \(\displaystyle (a,0)\), \(\displaystyle (a,b)\), \(\displaystyle (0,b)\). The plan is to cover the perimeter with circles of unit radius including four circles whose centers are \(\displaystyle (u,v)\), \(\displaystyle (a+u,v)\), \(\displaystyle (a+u, b+v)\), \(\displaystyle (u, b+v)\) for some \(\displaystyle u,v \leq \frac{1}{10}\), where the values of \(\displaystyle u\) and \(\displaystyle v\) are determined later. Consider that if, for example, the circle with center \(\displaystyle (u,v)\) is already covered, then from there we can determine the centers of the other circles that should be in this cover (the only complication could be near the vertices of the rectangle, but there we have specified what the centers of the circles in the cover will be). The circle centered at \(\displaystyle (u,v)\) covers the vertex \(\displaystyle (0,0)\) and around it a piece of the perimeter, and it intersects the \(\displaystyle x\) axis at the point \(\displaystyle (u+\sqrt{1-v^2},0)\). A circle must cover the point \(\displaystyle (u+\sqrt{1-v^2}+\varepsilon,0)\) for arbitrarily small \(\displaystyle \varepsilon\), which is only possible if there is another circle that passes through \(\displaystyle (u+\sqrt{1-v^2}, 0)\), so by the conditions of the problem the two circles must touch at this point, hence the centre of the other circle must be at \(\displaystyle (u+2\sqrt{1-v^2},-v)\). Similarly, it can be seen that this circle intersects the \(\displaystyle x\)-axis the second time at the point \(\displaystyle (u+3\sqrt{1-v^2},0)\), so there must be a next circle that touches it here, hence its centre must be at the point \(\displaystyle (u+4\sqrt{1-v^2},v)\). Continuing in this way, it can be seen that at each point \(\displaystyle (u+4k\sqrt{1-v^2},v)\) and \(\displaystyle (u+(4k+2)\sqrt{1-v^2},-v)\) there will be a center, where \(\displaystyle k\) is an integer and not too large, that is, until we reach the right side of the rectangle.
In order for \(\displaystyle (a+u,v)\) to be the center of a circle, it would have to be one of the centers listed above, i.e. of the form \(\displaystyle (u+4k\sqrt{1-v^2},v)\) for some positive integer \(\displaystyle k\). If this is satisfied, then the circles considered so far including this circle completely cover the lower side of the rectangle. This is satisfied if \(\displaystyle a=4k\sqrt{1-v^2}\). Let \(\displaystyle k=\left\lceil \frac{a}{4} \right\rceil\). Then from this we can express \(\displaystyle v\):
\(\displaystyle \sqrt{1-v^2}=\frac{a}{4k} \geq \frac{a}{a+4} \geq \sqrt{1-1/100},\)
\(\displaystyle \frac{a}{4k} \leq 1\) and \(\displaystyle \sqrt{1-v^2}\) is continuous, takes 1 at 0 and decreases monotonically at \(\displaystyle [0,1]\), so by the above inequalities there exists a unique \(\displaystyle v \in \left[0,\frac{1}{10}\right]\) satisfying the equality.
Doing the same for the right side of the rectangle, we obtain that the centers of the circles are \(\displaystyle (a+u,v+4k\sqrt{1-u^2})\) and \(\displaystyle (a-u, (4k+2)\sqrt{1-u^2})\), where \(\displaystyle k\) is an integer. Now we want \(\displaystyle (a+u,b+v)\) to be of such a form, i.e. \(\displaystyle b+v=v+4k\sqrt{1-u^2}\) for some integer \(\displaystyle k\). Similarly to the above reasoning, there exists a corresponding \(\displaystyle u \leq \frac{1}{10}\) and an integer \(\displaystyle k\) for which the equation is satisfied. It can be seen that if we choose \(\displaystyle u\) and \(\displaystyle v\) accordingly, then by defining the centers of the circles as in the above thought process, the top and left sides of the rectangle can be covered by circles, moreover \(\displaystyle (u,b+v)\) will be the center of a circle. So the only thing we need to check is that the circles do not intersect. Clearly, there could only be a problem around the vertices, and only if the two neighbours of the circle covering on of the vertices of the rectangle intersect, but by the choice \(\displaystyle u,v \leq \frac{1}{10}\) if \(\displaystyle O_1\), \(\displaystyle O_2\) and \(\displaystyle O_3\) are the centers of three adjacent circles in this order, then \(\displaystyle \angle O_1O_2O_3 \geq 60^{\circ}\), which means that the circles centered on \(\displaystyle O_1\) and \(\displaystyle O_3\) do not intersect.
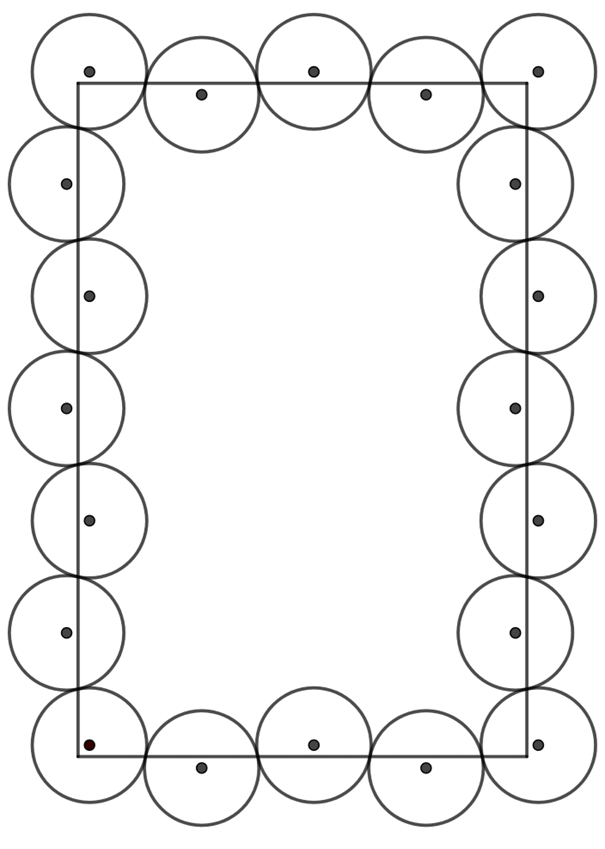
Second solution:
The basic idea is very similar to the previous solution, only now we want the points \(\displaystyle (u,v)\), \(\displaystyle (a-u,v)\), \(\displaystyle (a-u, b-v)\), \(\displaystyle (u, b-v)\) to be the centers of some circles in the covering for some \(\displaystyle \frac{1}{20} \leq u,v \leq \frac{1}{10}\). As in the previous solution, starting from the circle centered at \(\displaystyle (u,v)\) and covering the bottom side, the points \(\displaystyle (u+4k\sqrt{1-v^2},v)\) and \(\displaystyle (u+(4k+2)\sqrt{1-v^2}, -v)\) will be the centres of the circles, and we want \(\displaystyle (a-u,v)\) to be of this form, i.e. \(\displaystyle a-u=u+4k\sqrt{1-v^2}\) for some integer \(\displaystyle k\). In other words, we want \(\displaystyle \frac{a-2u}{4\sqrt{1-v^2}}\) to be an integer. Similarly, by covering the right side of the rectangle, we obtain the condition that \(\displaystyle \frac{b-2v}{4\sqrt{1-u^2}}\) should be an integer, and then, as in the previous solution, we can cover the upper and left sides according to the conditions, and the circles do not intersect if \(\displaystyle u, v \leq \frac{1}{10}\).
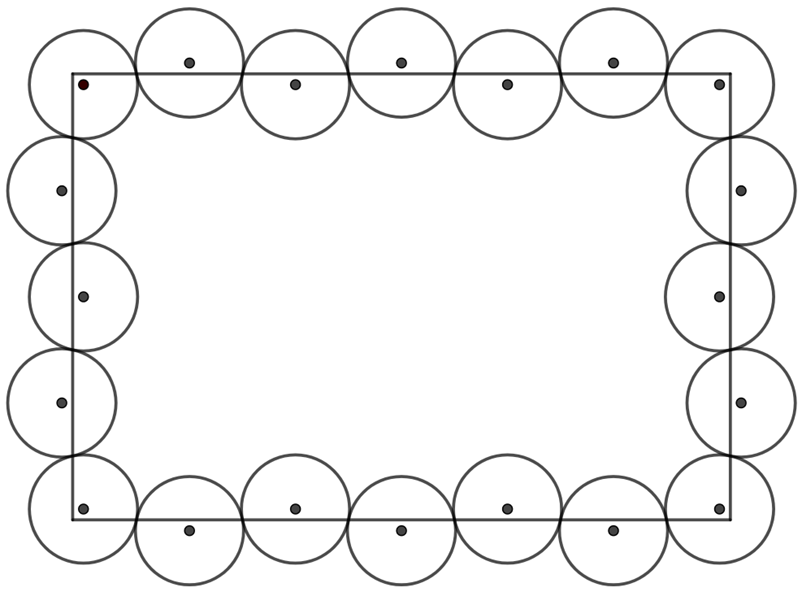
So we reduced the problem to finding \(\displaystyle \frac{1}{20} \leq u,v \leq \frac{1}{10}\) for which \(\displaystyle \frac{a-2u}{4\sqrt{1-v^2}}\) and \(\displaystyle \frac{b-2v}{4\sqrt{1-u^2}}\) are both integers. Consider \(\displaystyle f, g \ : \ \left[ \frac{1}{20}, \frac{1}{10} \right]^2 \to \mathbb{R}\), which order as described above, i.e. \(\displaystyle f(u,v)=\frac{a-2u}{4\sqrt{1-v^2}}\) and \(\displaystyle g(u,v)=\frac{b-2v}{4\sqrt{1-u^2}}\). We need to prove that there is a point when both functions take an integer.
Note the following about the functions. First, it is clear that \(\displaystyle f\) and \(\displaystyle g\) are continuous. Second, if \(\displaystyle a\) and \(\displaystyle b\) are large enough, then if \(\displaystyle u\) is changed a very little while \(\displaystyle v\) is left fixed, then \(\displaystyle f\) changes very little while \(\displaystyle g\) changes quite a bit. More precisely, we claim that if \(\displaystyle (u,v) \in \left[\frac{1}{20}, \frac{1}{10}\right]^2\) and \(\displaystyle \varepsilon>0\), and we shift \(\displaystyle u\) by \(\displaystyle \varepsilon\), i.e., we consider the pair \(\displaystyle (u+\varepsilon,v)\), where \(\displaystyle u+\varepsilon \leq \frac{1}{10}\) is still satisfied, then
\(\displaystyle |f(u,v)-f(u+\varepsilon,v)|\leq\varepsilon\ \text{ and } \ |g(u,v)-g(u+\varepsilon,v)|\geq 1000\varepsilon.\)
The first inequality is clear as in the function \(\displaystyle f\) the denominator is at least two, while the numerator changes by \(\displaystyle -2\varepsilon\). The proof of the second inequality is a bit more complicated. Let \(\displaystyle c=\frac{1/20}{\sqrt{1-1/400}}\), this is just the absolute value of the derivative of the function \(\displaystyle h(x)=\sqrt{1-x^2}\) at \(\displaystyle \frac{1}{20}\). Note that the function \(\displaystyle h(x)\) is just the equation of the unit circle centered at the origin, so it is concave on the interval \(\displaystyle \left[\frac{1}{20}, \frac{1}{10}\right]\), so its derivative is monotonically decreasing, hence the absolute value of the derivative is minimal in \(\displaystyle \frac{1}{20}\) on the interval \(\displaystyle \left[\frac{1}{20}, \frac{1}{10}\right]\), and there it is \(\displaystyle c\). For this reason
\(\displaystyle |h(u)-h(u+\varepsilon)| \geq c\varepsilon,\)
since, by Lagrange mean value theorem, there exists a \(\displaystyle t \in (u,u+\varepsilon)\) for which \(\displaystyle h'(t)=\frac{h(u+\varepsilon)-h(u)}{\varepsilon}\), and we know that \(\displaystyle |h'(t)| \geq c\). We reduce \(\displaystyle |g(u,v)-g(u+\varepsilon,v)|\) by decreasing their common numerator and increasing the denominator of each such that the difference of their denominators does not decrease, hence
\(\displaystyle |g(u,v)-g(u+\varepsilon,v)| \geq \frac{b-1}{4}-\frac{b-1}{4+c\varepsilon} = \frac{(b-1)(4+c\varepsilon)-4(b-1)}{4(4+c\varepsilon)} \geq \frac{(b-1)c\varepsilon}{20}.\)
From this we see that if \(\displaystyle N=\frac{20000}{c}+1\) and \(\displaystyle b>N\), then the second desired inequality is also satisfied.
Similarly, if \(\displaystyle v\) is changed by \(\displaystyle \varepsilon\), then \(\displaystyle f\) moves by at least \(\displaystyle 1000\varepsilon\), while \(\displaystyle g\) moves by at most \(\displaystyle \varepsilon\). Note also that if we increase \(\displaystyle u\), then \(\displaystyle f\) decreases and \(\displaystyle g\) increases, while if we increase \(\displaystyle v\), then \(\displaystyle f\) increases and \(\displaystyle g\) decreases. Now do the following: start from the point \(\displaystyle (x_0, y_0)=(\frac{1}{15},\frac{1}{15})\). Let's move along the \(\displaystyle x\) axis (i.e., increase \(\displaystyle u\)) until \(\displaystyle g\) becomes an integer, let this be the point \(\displaystyle (x_1,y_1)\). From the above observations, \(\displaystyle y_0=y_1\) and \(\displaystyle |x_1-x_0| \leq \frac{1}{1000}\). From here, increase the coordinate \(\displaystyle y\) until \(\displaystyle f\) is an integer, let the first such point be \(\displaystyle (x_2, y_2)\). Again, this is a step of at most \(\displaystyle \frac{1}{1000}\), so in the meantime \(\displaystyle g\) decreases by at most \(\displaystyle \frac{1}{1000}\). Now increase \(\displaystyle x\) again until \(\displaystyle g\) is an integer, let this be at the point \(\displaystyle (x_3, y_3)\). It can be seen that this requires moving \(\displaystyle x\) by at most \(\displaystyle \frac{1}{1000 \cdot 1000}\), so \(\displaystyle f\) decreases by at most that much, and in addition \(\displaystyle g(x_1,y_1)=g(x_3,y_3)\). And so on, alternately increasing the coordinates \(\displaystyle x\) and \(\displaystyle y\) to get the infinite series of points \(\displaystyle (x_n, y_n)\) for which \(\displaystyle g(x_1,y_1)=g(x_3,y_3)=g(x_5,y_5)= \ldots\) is an integer and \(\displaystyle f(x_2,y_2)=g(x_4,y_4)=g(x_6,y_6)= \ldots\) is also an integer. We see that in the \(\displaystyle n\)-th step, we move by at most \(\displaystyle \frac{1}{1000^{n-1}}\), so we never get out of the domain \(\displaystyle \left[\frac{1}{20}, \frac{1}{10}\right]^2\), and also the resulting series of points will converge to some point \(\displaystyle (x',y')\), and \(\displaystyle g(x',y')=g(x_1,y_1)\) is an integer and \(\displaystyle f(x',y')=f(x_2,y_2)\) is also an integer, just as we wanted.
Statistics:
6 students sent a solution. 7 points: Diaconescu Tashi, Lovas Márton, Németh Márton, Varga Boldizsár, Wiener Anna. 0 point: 1 student.
Problems in Mathematics of KöMaL, March 2023
