Problem A. 851. (April 2023)

A. 851. Let \(\displaystyle k\), \(\displaystyle l\) and \(\displaystyle m\) be positive integers. Let \(\displaystyle ABCDEF\) be a hexagon that has a center of symmetry whose angles are all \(\displaystyle 120^{\circ}\) and let its sidelengths be \(\displaystyle AB=k\), \(\displaystyle BC=l\) and \(\displaystyle CD=m\). Let \(\displaystyle f(k,l,m)\) denote the number of ways we can partition hexagon \(\displaystyle ABCDEF\) into rhombi with unit sides and an angle of \(\displaystyle 120^{\circ}\).

Prove that by fixing \(\displaystyle l\) and \(\displaystyle m\), there exists polynomial \(\displaystyle g_{l,m}\) such that \(\displaystyle f(k,l,m)=g_{l,m}(k)\) for every positive integer \(\displaystyle k\), and find the degree of \(\displaystyle g_{l,m}\) in terms of \(\displaystyle l\) and \(\displaystyle m\).

Submitted by Zoltán Gyenes, Budapest

(7 pont)

Deadline expired on May 10, 2023.

Let's assume that the hexagon is somehow tiled with rhombi, and consider the two opposite sides of length \(\displaystyle k\). It can be seen that there are \(\displaystyle k\) paths from one side to the other such that we pass through the midlines of the rhombi that connect two opposite midpoints parallel to the \(\displaystyle k\)-long side. These paths cannot intersect each other, so each path takes exactly \(\displaystyle l\) steps in one direction and \(\displaystyle m\) steps in the other direction. Let's consider the hexagon such that the \(\displaystyle k\)-long side is horizontal, and let's call the two types of steps on the paths right (R) and left (L) steps, with \(\displaystyle l\) R steps always present. Then, the fact that they don't intersect means that if we look at a path, for every \(\displaystyle t\), in the first \(\displaystyle t\) steps the path can step to the right at most as many times as the path to its right. That is, if we write the R-L sequences that describe the paths below each other in the rows of a \(\displaystyle k\)-row and \(\displaystyle l+m\)-column table, then for any two rows and number \(\displaystyle t\), it must be true that there are at least as many R's in the first \(\displaystyle t\) positions in the lower row as in the upper one. Conversely, it is easy to see that such a table corresponds to paths that do not intersect, and such paths uniquely determine a tiling with rhombi. Thus, the problem is equivalent to proving that the number of such tables is a polynomial in \(\displaystyle k\).

(In the picture, B represents L and J represents R, based on the Hungarian names.)

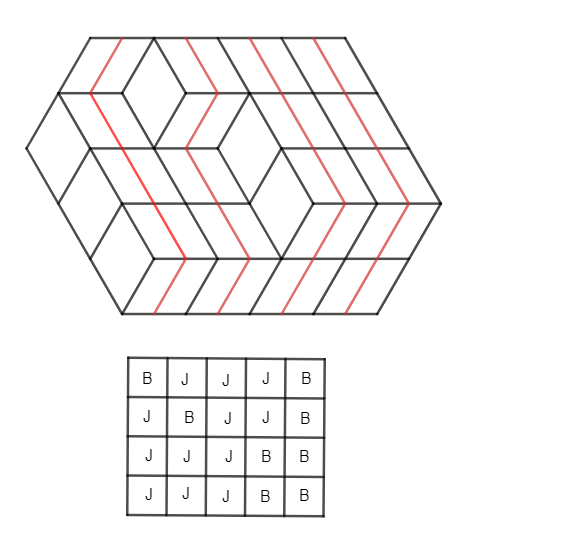
Consider the R-L sequences of length \(\displaystyle l+m\) containing exactly \(\displaystyle l\) R's. Let's define a partial order on these sequences such that one sequence is smaller than another if it can be placed above it in the table (i.e., it has at most as many R's in any initial slice as the other). It is clear that this property is transitive. Let \(\displaystyle P\) be the resulting partially ordered set. Then we can count the appropriate tables as follows: take an arbitrary non-empty chain \(\displaystyle L\) from \(\displaystyle P\), suppose it has \(\displaystyle s_L\) elements. Then the tables containing exactly these rows correspond to \(\displaystyle \binom{k-1}{s_L-1}\), since the partial order determines the order of the rows, so we can only decide how many of each there should be, thus we need to insert \(\displaystyle s_L-1\) separator lines among the \(\displaystyle k\) rows. The condition states that the set of R-L sequences in a table must form a chain in \(\displaystyle P\), so summing the above expression \(\displaystyle \binom{k-1}{s_L-1}\) over all chains \(\displaystyle L\) in \(\displaystyle P\) gives the desired quantity.

Since \(\displaystyle l\) and \(\displaystyle m\) are fixed, we sum a fixed number of terms of the form \(\displaystyle \binom{k-1}{s_L-1}\), which are polynomials of degree \(\displaystyle s_L-1\) in \(\displaystyle k\). Thus, \(\displaystyle f(k,l,m)\) is indeed a polynomial in \(\displaystyle k\), with its degree being the length of the longest chain in \(\displaystyle P\) minus 1.

Assign to each sequence the number of (R, L) pairs for which R precedes L. This is \(\displaystyle 0\) for the sequence starting with \(\displaystyle m\) letters L, and \(\displaystyle lm\) for the sequence ending with \(\displaystyle m\) letters L, and falls between these values for all other sequences. It can be seen that if a sequence in \(\displaystyle P\) is larger than another, then this assigned value is also larger, so the length of a chain can be at most \(\displaystyle lm+1\). And this is indeed achievable, for example, if we start with the sequence beginning with \(\displaystyle m\) letters L, then successively move the rightmost L to the end, followed by the next L, and so on, until we reach the point where all L's are at the end of the sequence. Therefore, \(\displaystyle lm+1\) is the length of the longest chain in \(\displaystyle P\), making \(\displaystyle f(k,l,m)\) an \(\displaystyle lm\)-degree polynomial in \(\displaystyle k\).

Statistics:

5 students sent a solution.
7 points:	Sida Li, Varga Boldizsár.
5 points:	1 student.
2 points:	1 student.
0 point:	1 student.

Problems in Mathematics of KöMaL, April 2023