 Problem A. 853. (April 2023)
Problem A. 853. (April 2023)
A. 853. Let points \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle A'\), \(\displaystyle B'\), \(\displaystyle C'\) be chosen in the plane such that no three of them are collinear, and let lines \(\displaystyle AA'\), \(\displaystyle BB'\), \(\displaystyle CC'\) be tangent to a given equilateral hyperbola at points \(\displaystyle A\), \(\displaystyle B\) and \(\displaystyle C\), respectively. Assume that the circumcircle of \(\displaystyle A'B'C'\) is the same as the nine-point circle of triangle \(\displaystyle ABC\). Let \(\displaystyle s(A')\) be the Simson line of point \(\displaystyle A'\) with respect to the pedal triangle of \(\displaystyle ABC\). Let \(\displaystyle A^*\) be the intersection of line \(\displaystyle B'C'\) and the perpendicular of \(\displaystyle s(A')\) through point \(\displaystyle A\). Points \(\displaystyle B^*\) and \(\displaystyle C^*\) are defined in a similar manner. Prove that points \(\displaystyle A^*\), \(\displaystyle B^*\) and \(\displaystyle C^*\) are collinear.
Submitted by Áron Bán-Szabó, Budapest
(7 pont)
Deadline expired on May 10, 2023.
The solution of this problem is based on the following three lemmas:
Lemma 1: The isogonal conjugate of point \(\displaystyle P\) on the circumcircle of a given triangle is an ideal point that is perpendicular to the Simson-line of \(\displaystyle P\) with respect to the triangle.
Lemma 2: The isogonal conjugate of an arbitrary point with respect to the pedal triangle of \(\displaystyle ABC\) is on the polar of the original point with respect to the hyperbola.
Lemma 3: Taking the polars of the vertices of a triangle with respect to a given conic the triangle defined by the polars is perspective with the original triangle.
Let's see how these lemmas solve the problem. The polar \(\displaystyle p(A')\) of point \(\displaystyle A'\) with respect to hyperbola goes through point \(\displaystyle A\) because of \(\displaystyle AA'\) being tangent to the hyperbola. By lemma 2, we also know that the isogonal conjugate of \(\displaystyle A'\) with respect to the pedal triangle is on \(\displaystyle p(A')\). By lemma 1, we also know that the isogonal conjugate of \(\displaystyle A'\) is the ideal point that is perpendicular to \(\displaystyle s(A')\). Combining these we get that \(\displaystyle p(A')\) is the line through \(\displaystyle A\) that is perpendicular to \(\displaystyle s(A')\), i.e line \(\displaystyle AA^*\). By lemma 3 triangle \(\displaystyle A'B'C'\) and the triangle defined by lines \(\displaystyle p(A')\), \(\displaystyle p(B')\) and \(\displaystyle p(C')\) are perspective, so by Desargues' theorem their respective sides intersect each other in three collinear points, but these intersection points are exactly \(\displaystyle A^*\), \(\displaystyle B^*\) and \(\displaystyle C^*\).
Proof of lemma 3: let the triangle be \(\displaystyle A'B'C'\), and let the polars of the vertices intersect the respective sides in \(\displaystyle A^*\), \(\displaystyle B^*\) and \(\displaystyle C^*\). Let the pole of line \(\displaystyle A'B'\) be \(\displaystyle K\), and let the polar of \(\displaystyle B'\) intersect lines \(\displaystyle A'B'\) and \(\displaystyle B'C'\) in \(\displaystyle M\) and \(\displaystyle N\), respectively.
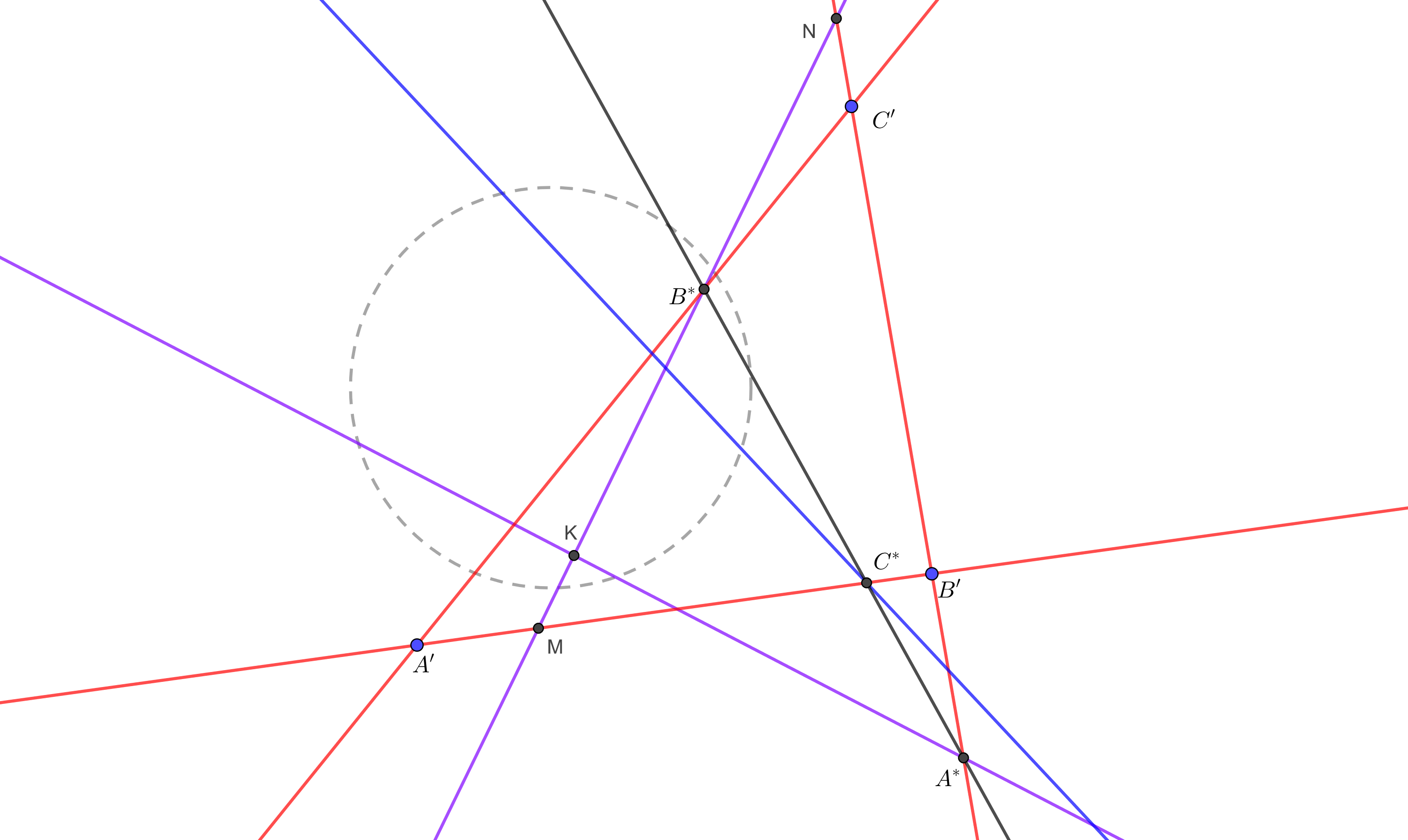
If we project line \(\displaystyle A'B'\) to line \(\displaystyle B'C'\) through \(\displaystyle B^*\), we can observe that \(\displaystyle A'\) is mapped to \(\displaystyle C'\), \(\displaystyle M\) to \(\displaystyle N\) and \(\displaystyle B'\) to \(\displaystyle B'\). Since projections preserve cross ratio, in order to show that \(\displaystyle C^*\) is mapped to \(\displaystyle A^*\) we have to prove that cross ratios \(\displaystyle (A',M;C^*,B')\) and \(\displaystyle (C',N;A^*,B')\) are equal. Now let's take advantage of the fact that the pole-polar map also preserves the cross ratio. Now the polar of \(\displaystyle M\) is \(\displaystyle KB'\): using La Hire's theorem we see that \(\displaystyle K\) is on the polar of \(\displaystyle M\) since \(\displaystyle M\) is on \(\displaystyle A'B'\), the pole of which is \(\displaystyle K\), and \(\displaystyle B'\) is on the polar of \(\displaystyle M\) since \(\displaystyle M\) is on the polar of \(\displaystyle B'\), which is line \(\displaystyle MN\) by definition. Similarly, using La Hire's theorem again the polar of \(\displaystyle C^*\) is \(\displaystyle KC'\): \(\displaystyle K\) is on the polar of \(\displaystyle C^*\) since \(\displaystyle C^*\) is on \(\displaystyle A'B'\), the pole of which is \(\displaystyle K\), and \(\displaystyle C'\) is on the polar of \(\displaystyle C^*\), since \(\displaystyle C^*\) is on the polar of \(\displaystyle C'\) by definition. Thus cross ratio \(\displaystyle (A',M;C^*,B')\) is the same as the cross ratio of lines \(\displaystyle (KA^*,KB';KC',KN)\) which is the same as the cross ratio of points \(\displaystyle (A^*,B';C',N)\). Now based on well known identities about cross ratios we get that \(\displaystyle (A^*,B';C',N)=(C',N;A^*,B')\), which is what we wanted to prove.
Proof of lemma 2: we will use the well known fact that if the vertices of a triangle is on an equilateral hyperbola, then the orthocenter of the triangle will also be on the hyperbola. Let \(\displaystyle H\) denote the orthocenter of triangle \(\displaystyle ABC\) that is also on the hyperbola given in the problem. Also, let the isogonal conjugate of \(\displaystyle P\) be \(\displaystyle Q\) with respect to the pedal triangle (\(\displaystyle DEF\) on the figure).
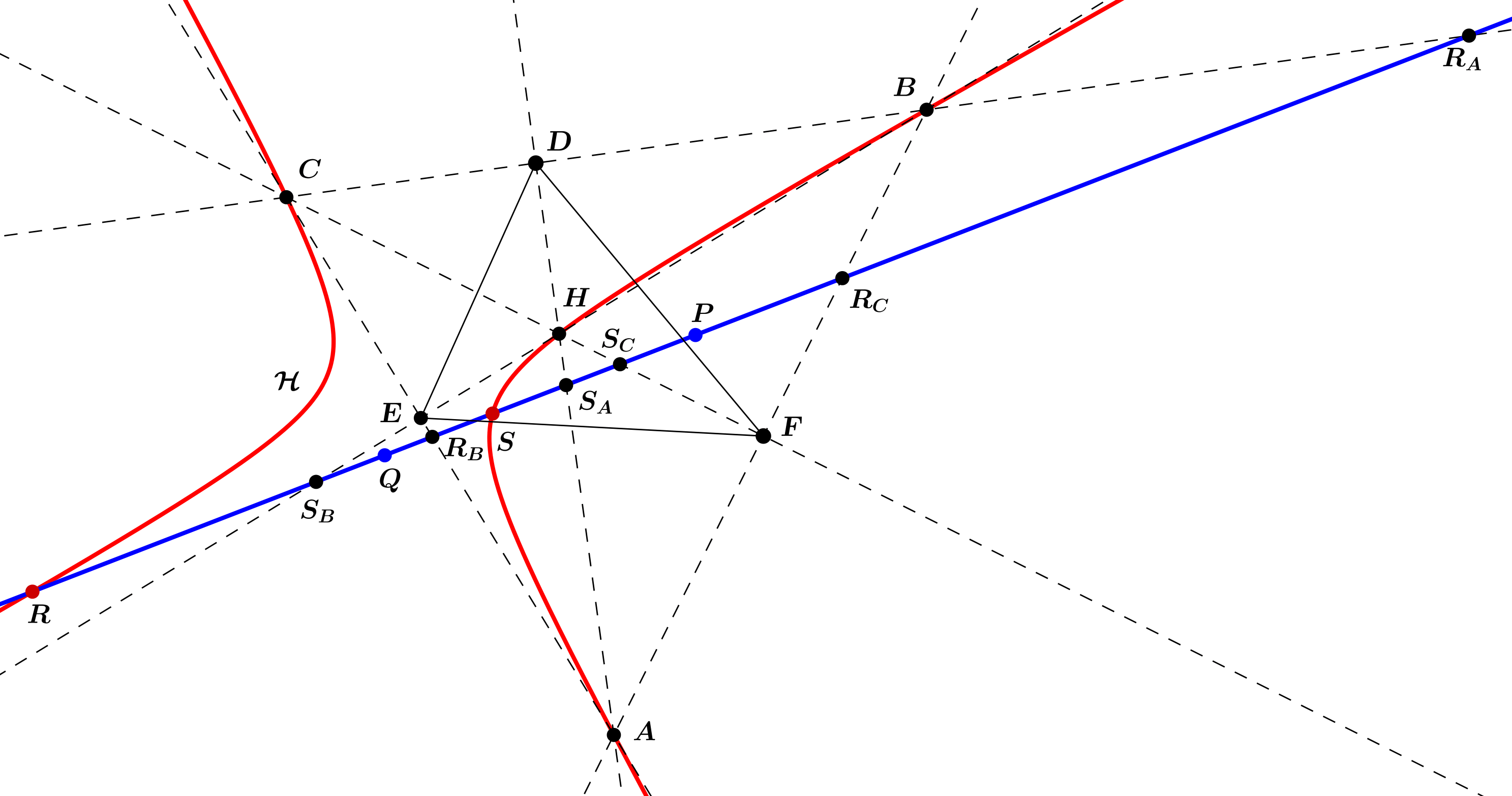
Now consider the following transformation \(\displaystyle t\) on line \(\displaystyle PQ\): let point \(\displaystyle X\) be mapped to the second intersection of line \(\displaystyle PQ\) and the conic through points \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle H\) and \(\displaystyle X\). Applying Pascal's theorem to hexagon \(\displaystyle ABCHXX'\) we can verify that this transformation is projective (it preserves the cross ratio): points \(\displaystyle AB\cap HX=X_1\), \(\displaystyle BC\cap XX'=S\) and \(\displaystyle CH\cap X'A=X_2\) are collinear. Now note that \(\displaystyle BC\cap XX'=BC\cap PQ=S\) is independent from the choice of \(\displaystyle X\). Now \(\displaystyle X'\) can be obtained from \(\displaystyle X\) using three projections: first project \(\displaystyle X\) through \(\displaystyle H\) to \(\displaystyle AB\) to get \(\displaystyle AB\cap HX=X_1\). Now project \(\displaystyle X_1\) through \(\displaystyle S\) to \(\displaystyle CH\) to get \(\displaystyle CH\cap X'A=X_2\). Finally project \(\displaystyle X_2\) through \(\displaystyle A\) to \(\displaystyle PQ\) to get \(\displaystyle X'\).
Now let line \(\displaystyle PQ\) intersect lines \(\displaystyle BC,AD,CA,BE,AB,CF\) in \(\displaystyle R_A,S_A,R_B,S_B,R_C,S_C\), respectively. By the definition of the isogonal conjugate \(\displaystyle DP\) and \(\displaystyle DQ\) are symmetric to lines \(\displaystyle DA\) and \(\displaystyle BC\), thus \(\displaystyle DA\) and \(\displaystyle BC\) bisects angle \(\displaystyle PDQ\). It is well know that \(\displaystyle DA\), \(\displaystyle BC\), \(\displaystyle DP\) and \(\displaystyle DQ\) are harmonic, and thus their intersections with \(\displaystyle PQ\), i.e. points \(\displaystyle S_A\), \(\displaystyle R_A\), \(\displaystyle P\) and \(\displaystyle Q\) are also harmonic. However, note that \(\displaystyle R_A\) and \(\displaystyle S_A\) are mapped to each other by transformation \(\displaystyle t\): the conic through \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle H\) and \(\displaystyle S_A\) is just lines \(\displaystyle DA\) and \(\displaystyle BC\). The same is true for pairs \(\displaystyle S_B\), \(\displaystyle R_B\) and \(\displaystyle S_C\), \(\displaystyle R_C\). Since a projective transformation on a line is defined by three points, this means that transformation \(\displaystyle t\) is the harmonic conjugation with respect to \(\displaystyle P\) and \(\displaystyle Q\), and this proves our statement when we apply it to our original hyperbola.
Lemma 1 is quite well known, and it can be proved by some angle chasing, which we leave to the reader.
Statistics:
2 students sent a solution. 1 point: 1 student. 0 point: 1 student.
Problems in Mathematics of KöMaL, April 2023
