Problem A. 855. (May 2023)

A. 855. In scalene triangle \(\displaystyle ABC\) the shortest side is \(\displaystyle BC\). Let points \(\displaystyle M\) and \(\displaystyle N\) be chosen on sides \(\displaystyle AB\) and \(\displaystyle AC\), respectively, such that \(\displaystyle BM=CN=BC\). Let \(\displaystyle I\) and \(\displaystyle O\) denote the incenter and circumcentre of triangle \(\displaystyle ABC\), and let \(\displaystyle D\) and \(\displaystyle E\) denote the incenter and circumcenter of triangle \(\displaystyle AMN\). Prove that lines \(\displaystyle IO\) and \(\displaystyle DE\) intersect each other on the circumcircle of triangle \(\displaystyle ABC\).

Submitted by Luu Dong, Vietnam

(7 pont)

Deadline expired on June 12, 2023.

Let \(\displaystyle H\) denote the second intersection point of circles \(\displaystyle ABC\) and \(\displaystyle AMN\). It is well known that this point is the center of the spiral symmetry that maps line segment \(\displaystyle MB\) to \(\displaystyle NC\). However, this two line segments have the same length, thus the spiral symmetry is a rotation. This implies \(\displaystyle HM=HN\) and \(\displaystyle HB=HC\).

Let ray \(\displaystyle IO\) intersect circle \(\displaystyle (ABC)\) at point \(\displaystyle K\). Let \(\displaystyle F\) and \(\displaystyle G\) be the diametrically opposite points of \(\displaystyle H\) in circles \(\displaystyle (AMN)\) and \(\displaystyle (ABC)\). It is well known, that these points are on the common internal angle bisector of \(\displaystyle \angle MAN\) and \(\displaystyle \angle BAC\), which also contains points \(\displaystyle D\) and \(\displaystyle I\).

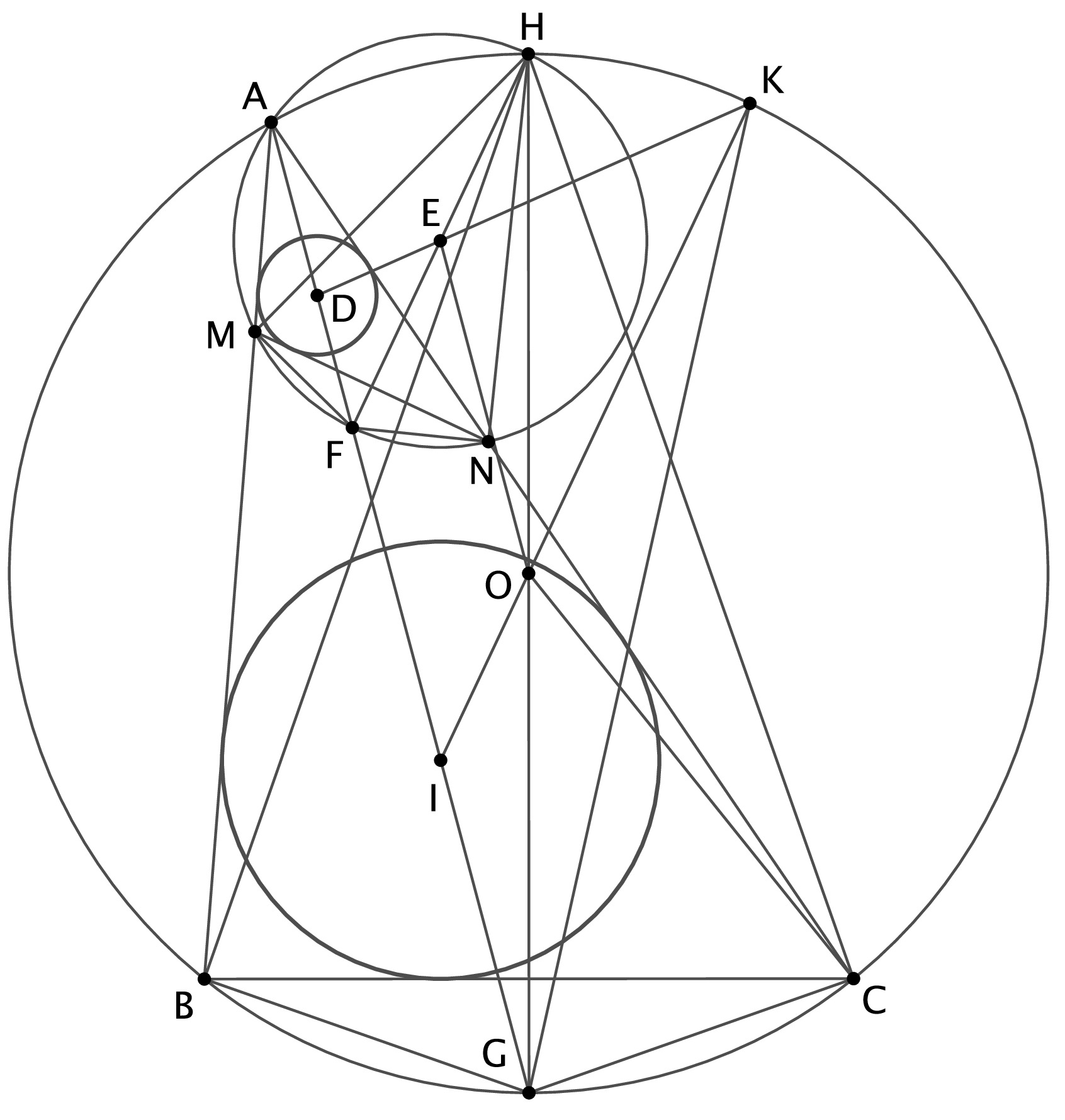
It's well known (and simple angle chasing shows) that triangles \(\displaystyle HBC\), \(\displaystyle OGC\), \(\displaystyle MHN\) and \(\displaystyle EFN\) are similar. Using this, noticing that \(\displaystyle \angle IGO=\angle NCH=(\gamma-\beta)/2\) and taking advantage of the fact that \(\displaystyle CB=CN\) (and thus \(\displaystyle GI/GO=GC/GO=CB/CH=CN/CH)\) we get that triangles \(\displaystyle IGO\) and \(\displaystyle NCH\) are also similar to each other. This finally implies that \(\displaystyle EF\) and \(\displaystyle IO\) are parallel to each other: \(\displaystyle \angle GFH = \pi - \angle AFH = \pi - \angle ANH = \angle CNH = \angle GIO\).

Now the last thing to observe is that quadrilateral \(\displaystyle FIOE\) is a parallelogram. We have already seen the \(\displaystyle EF\) and \(\displaystyle IO\) are parallel to each other. Since triangles \(\displaystyle IGO\) and \(\displaystyle NCH\) are similar to each other, \(\displaystyle IO/OG=NH/HC\). Since triangles \(\displaystyle MNH\) and \(\displaystyle BCH\) are also similar, \(\displaystyle OG/HC=EF/NH\). Multiplying these two ratios together we get that \(\displaystyle IO/HC=EF/HC\), thus \(\displaystyle IO=EF\), and this proves our claim.

Using all these it is easy to prove the claim of the original problem. Using some of the results from above we have that

\(\displaystyle \frac{DF}{FE} = \frac{FN}{FE} = \frac{GC}{GO} = \frac{EO}{OK}. \)

Now focusing on triangles \(\displaystyle DFE\) and \(\displaystyle EOK\) we have two pairs of parallel sides and an equal ratio of sides thus they must be similar. But this implies the the third pair of sides being also parallel, this \(\displaystyle D\), \(\displaystyle E\) and \(\displaystyle K\) are collinear, what we had to prove.

Statistics:

8 students sent a solution.
7 points:	Bodor Mátyás, Foris Dávid, Sida Li, Varga Boldizsár, Wiener Anna.
6 points:	Lovas Márton.
5 points:	1 student.
Unfair, not evaluated:	1 solutions.

Problems in Mathematics of KöMaL, May 2023