Problem A. 857. (September 2023)

A. 857. Let \(\displaystyle ABC\) be a given acute triangle, in which \(\displaystyle BC\) is the longest side. Let \(\displaystyle H\) be the orthocenter of the triangle, and let \(\displaystyle D\) and \(\displaystyle E\) be the feet of the altitudes from \(\displaystyle B\) and \(\displaystyle C\), respectively. Let \(\displaystyle F\) and \(\displaystyle G\) be the midpoints of sides \(\displaystyle AB\) and \(\displaystyle AC\), respectively. \(\displaystyle X\) is the point of intersection of lines \(\displaystyle DF\) and \(\displaystyle EG\). Let \(\displaystyle O_1\) and \(\displaystyle O_2\) be the circumcenters of triangles \(\displaystyle EFX\) and \(\displaystyle DGX\), respectively. Finally, \(\displaystyle M\) is the midpoint of line segment \(\displaystyle O_1O_2\). Prove that points \(\displaystyle X\), \(\displaystyle H\) and \(\displaystyle M\) are collinear.

Proposed by Boldizsár Varga, Verőce

(7 pont)

Deadline expired on October 10, 2023.

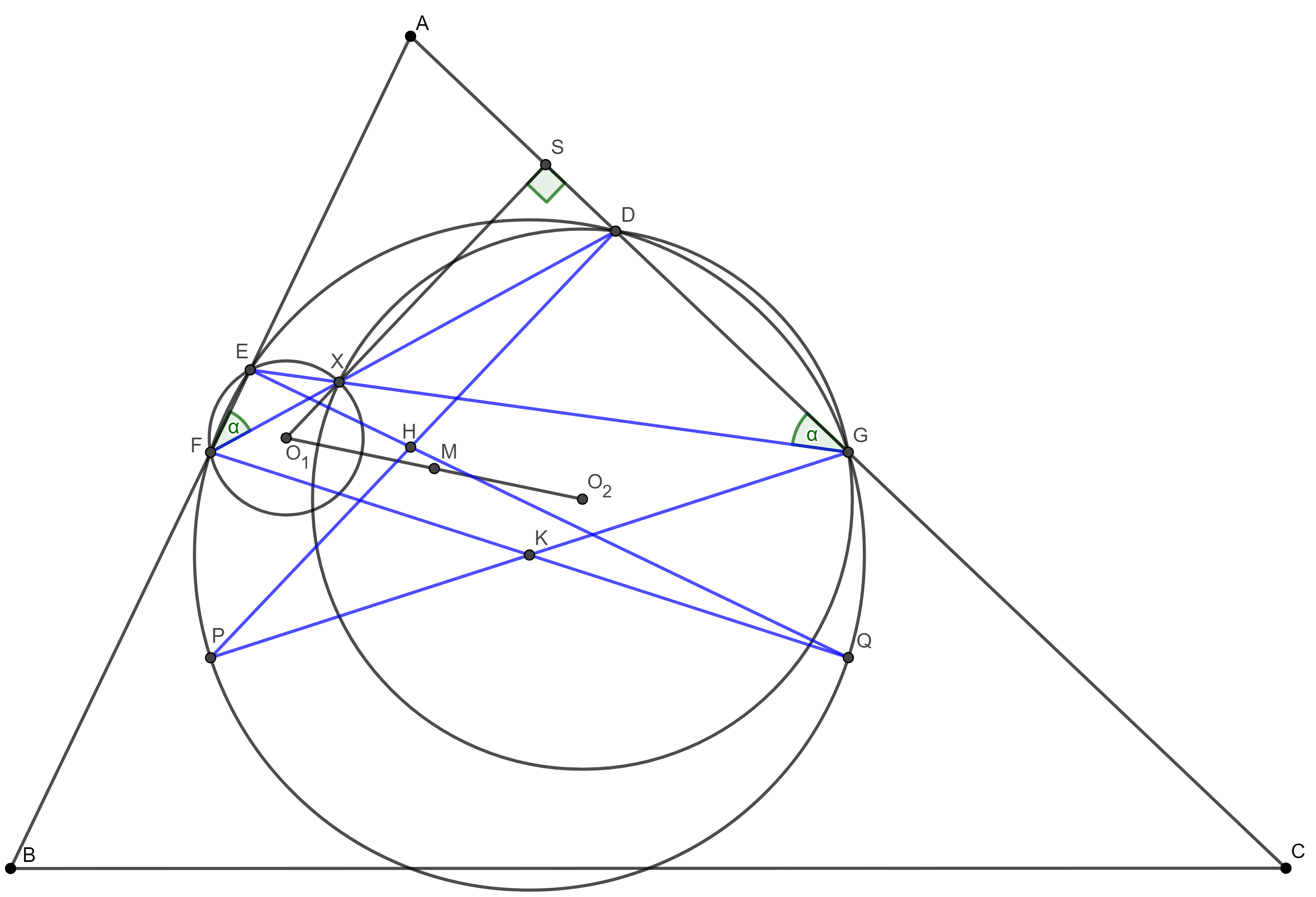
We will show that all three points lie on the Euler line of triangle \(\displaystyle ABC\). It is known that \(\displaystyle H\) does, so it is sufficient to prove this for \(\displaystyle M\) and \(\displaystyle X\).

Let \(\displaystyle K\) be the center of the Feuerbach circle of triangle \(\displaystyle ABC\). It is known that \(\displaystyle K\) also lies on the Euler line of triangle \(\displaystyle ABC\). Let \(\displaystyle P\) and \(\displaystyle Q\) be the second intersection points of the Feuerbach circle with segments \(\displaystyle BD\) and \(\displaystyle CE\), respectively. It is known that \(\displaystyle D,\) \(\displaystyle E,\) \(\displaystyle F,\) and \(\displaystyle G\) lie on the Feuerbach circle. Since \(\displaystyle \angle FEQ = 90^{\circ}\), it follows from the Thales' theorem that \(\displaystyle Q\) is the point opposite to \(\displaystyle F\) and similarly, \(\displaystyle P\) is opposite to \(\displaystyle G\) on the Feuerbach circle. Therefore, lines \(\displaystyle FQ\) and \(\displaystyle GP\) pass through point \(\displaystyle K\). Applying Pascal's theorem to the hexagon \(\displaystyle EQFDPG\) inscribed in the Feuerbach circle, we get that lines \(\displaystyle EQ\cap DP = H,\) \(\displaystyle QF\cap PG = K,\) and \(\displaystyle FD\cap GE = X\) are collinear, which means that \(\displaystyle X\) also lies on the Euler line of triangle \(\displaystyle ABC\).

We finish the proof by showing that \(\displaystyle M\) is the midpoint of segment \(\displaystyle XK\). To prove this, we show that quadrilateral \(\displaystyle XO_1KO_2\) is a parallelogram, furthermore, its opposite sides are perpendicular to lines \(\displaystyle AC\) and \(\displaystyle AB\). Due to symmetry, it is sufficient to prove this for lines \(\displaystyle O_2K\) and \(\displaystyle O_1X\). It is clear that \(\displaystyle O_2K\) satisfies this condition since both \(\displaystyle O_2\) and \(\displaystyle K\) lie on the perpendicular bisector of segment \(\displaystyle DG\). Let \(\displaystyle S\) be the intersection of line \(\displaystyle O_1X\) and \(\displaystyle AC\), and let \(\displaystyle \angle DGE = \alpha\). Then, \(\displaystyle \angle DFE = \alpha\) since \(\displaystyle GDEF\) is a cyclic quadrilateral. From the fact that \(\displaystyle \angle XO_1E = 2\alpha\) since it is a central angle in the circumcircle of triangle \(\displaystyle XEF\), we have \(\displaystyle \angle EXO_1 = 90^{\circ}-\alpha\). Hence \(\displaystyle \angle GXS=90^{\circ}-\alpha\), which implies that \(\displaystyle \angle XSG\) is a right angle, as desired.

Statistics:

25 students sent a solution.
7 points:	Anay Aggarwal, Bencz Benedek, Bodor Mátyás, Chrobák Gergő, Czanik Pál, Diaconescu Tashi, Duchon Márton, Farkas 005 Bendegúz, Fleischman Illés, Foris Dávid, Forrai Boldizsár, Gömze Norken, Hodossy Réka, Kovács Benedek Noel, Lincoln Liu, Selim Cadîr, Simon László Bence, Tarján Bernát, Varga Boldizsár, Virág Lénárd Dániel, Virág Rudolf, Wiener Anna.
6 points:	Philip Stefanov.
4 points:	1 student.
3 points:	1 student.

Problems in Mathematics of KöMaL, September 2023