Problem A. 862. (October 2023)

A. 862. Let \(\displaystyle ABCD\) be a cyclic quadrilateral inscribed in circle \(\displaystyle \omega\). Let \(\displaystyle F_A\), \(\displaystyle F_B\), \(\displaystyle F_C\) and \(\displaystyle F_D\) be the midpoints of arcs \(\displaystyle AB\), \(\displaystyle BC\), \(\displaystyle CD\) and \(\displaystyle DA\) of \(\displaystyle \omega\). Let \(\displaystyle I_A\), \(\displaystyle I_B\), \(\displaystyle I_C\) and \(\displaystyle I_D\) be the incenters of triangles \(\displaystyle DAB\), \(\displaystyle ABC\), \(\displaystyle BCD\) and \(\displaystyle CDA\), respectively.

Let \(\displaystyle \omega_A\) denote the circle that is tangent to \(\displaystyle omega\) at \(\displaystyle F_A\) and also tangent to line segment \(\displaystyle CD\). Similarly, let \(\displaystyle \omega_C\) denote the circle that is tangent to \(\displaystyle \omega\) at \(\displaystyle F_C\) and tangent to line segment \(\displaystyle AB\).

Finally, let \(\displaystyle T_B\) denote the second intersection of \(\displaystyle \omega\) and circle \(\displaystyle F_BI_BI_C\) different from \(\displaystyle F_B\), and let \(\displaystyle T_D\) denote the second intersection of \(\displaystyle \omega\) and circle \(\displaystyle F_DI_DI_A\).

Prove that the radical axis of circles \(\displaystyle \omega_A\) and \(\displaystyle \omega_C\) passes through points \(\displaystyle T_B\) and \(\displaystyle T_D\).

Submitted by Géza Kós, Budapest

(7 pont)

Deadline expired on November 10, 2023.

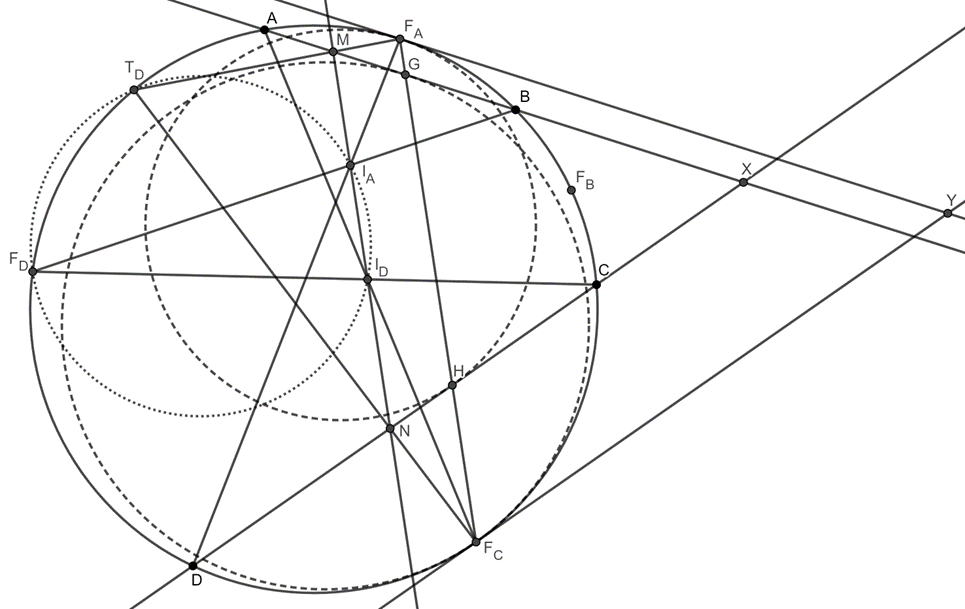
We will show that the radical axis passes through point \(\displaystyle T_D\), a similar argument will work for \(\displaystyle T_D\). Our solution does not work when \(\displaystyle AB\) and \(\displaystyle CD\) are parallel: in this case \(\displaystyle X\) and \(\displaystyle Y\) coincide (both are the ideal point), and in our solution we will need the line formed by them. The problem is hard even when \(\displaystyle AB\) and \(\displaystyle CD\) are parallel to each other. In this solution we will give a non-rigorous proof for this case. Suppose that the statement turned out to be true when \(\displaystyle AB\) and \(\displaystyle CD\) are not parallel to each other. If we fix \(\displaystyle A\), \(\displaystyle B\) and \(\displaystyle C\), and move \(\displaystyle D\) on the circumcircle of \(\displaystyle ABC\), it can be proved that the radical axis and point \(\displaystyle T_D\) both move continuously. Thus it has to true in the case \(\displaystyle AB\) and \(\displaystyle CD\) are parallel, too.

From now on let's assume that \(\displaystyle AB\) and \(\displaystyle CD\) are not parallel to each other, and let \(\displaystyle X\) be the intersection of these lines. The tangents at \(\displaystyle F_A\) and \(\displaystyle F_C\) also intersect each other, let their intersection be \(\displaystyle Y\). The first key statement is that the radical axis of circles \(\displaystyle \omega_A\) and \(\displaystyle \omega_C\) is \(\displaystyle XY\). Since \(\displaystyle Y\) is the radical center of circles \(\displaystyle \omega_A\), \(\displaystyle \omega_C\) and circle \(\displaystyle ABCD\), thus it has to be on the radical axis of \(\displaystyle \omega_A\) and \(\displaystyle \omega_C\).

Now let's show the same for point \(\displaystyle X\). Let points \(\displaystyle H\) and \(\displaystyle G\) be the points of tangency of \(\displaystyle \omega_A\) and \(\displaystyle \omega_C\) on \(\displaystyle CD\) and \(\displaystyle AB\), respectively. If we enlarge circle \(\displaystyle \omega_A\) from point \(\displaystyle F_A\) such that we get circle \(\displaystyle ABCD\), the image of \(\displaystyle H\) will \(\displaystyle F_C\). This shows that \(\displaystyle F_A\), \(\displaystyle H\) and \(\displaystyle F_C\) are collinear, and \(\displaystyle CD\) and \(\displaystyle F_CY\) are parallel to each other. Similarly, \(\displaystyle AB\) and \(\displaystyle F_AY\) are parallel, and \(\displaystyle G\) is on line segment \(\displaystyle F_AF_C\). Thus triangles \(\displaystyle HGX\) and \(\displaystyle F_AF_CY\) are similar. This implies \(\displaystyle GX=HX\) (from \(\displaystyle F_AY=F_CY\)), thus the tangents from \(\displaystyle X\) to circles \(\displaystyle \omega_A\) and \(\displaystyle \omega_C\) have the same length, and so \(\displaystyle X\) is on the radical axis of \(\displaystyle \omega_A\) and \(\displaystyle \omega_C\).

We will use the following two well known facts about the incenters: a vertex, the incenter and the midpoint of the opposite arc are collinear, and the midpoint of an arc has the same distance from the two adjacent vertices and the incenter. Thus triples\(\displaystyle (B,I_A,F_D)\), \(\displaystyle (C,I_D,F_D)\), \(\displaystyle (D,I_A,F_A)\) and \(\displaystyle (A,I_D,F_C)\) are collinear, and \(\displaystyle F_DA=F_DI_A=F_DD\) and \(\displaystyle F_DA=F_DI_D=F_DD\), and thus points \(\displaystyle A\), \(\displaystyle I_A\), \(\displaystyle I_D\) and \(\displaystyle D\) are on circle with center \(\displaystyle F_D\).

Applying inscribed angle theorem in circles \(\displaystyle AI_AI_DD\) and \(\displaystyle ABCD\), we get that \(\displaystyle \angle DI_AI_D=\angle DAI_D=\angle DAF_C=DF_AF_C\), which implies \(\displaystyle I_AI_D\) and \(\displaystyle F_AF_C\) are parallel.

Considering the radical center of circles \(\displaystyle AI_AI_DD\), \(\displaystyle ABCD\) and \(\displaystyle F_DT_DI_AI_D\) we get that lines \(\displaystyle T_DF_D\), \(\displaystyle AD\) and \(\displaystyle I_AI_D\) are concurrent. Let's apply Pascal's theorem to hexagon \(\displaystyle DABF_DT_DF_A\). We get that points \(\displaystyle DA\cap F_DT_D\), \(\displaystyle M=AB\cap T_DF_A\) and \(\displaystyle I_A=BF_D\cap F_AD\) are collinear. Similarly we get that point \(\displaystyle N=CD\cap F_CT_D\) is also on \(\displaystyle IAI_D\).

Thus line \(\displaystyle MN\) is parallel to line \(\displaystyle F_AF_C\), and so triangles \(\displaystyle NMX\) and \(\displaystyle F_CF_AY\) have parallel sides, thus they have a center of similarity, implying lines \(\displaystyle NF_C\), \(\displaystyle M_FA\) and \(\displaystyle XY\) are concurrent. However, we have just proved that two of these intersect each other in \(\displaystyle T_D\), and \(\displaystyle XY\) is the radical axis of circles \(\displaystyle \omega_A\) and \(\displaystyle \omega_C\), and this is what we wanted to prove.

Statistics:

13 students sent a solution.
7 points:	Bodor Mátyás, Diaconescu Tashi, Foris Dávid, Philip Stefanov, Simon László Bence, Varga Boldizsár, Virág Rudolf, Wiener Anna, Zömbik Barnabás.
3 points:	2 students.
2 points:	1 student.
Not shown because of missing birth date or parental permission:	1 solutions.

Problems in Mathematics of KöMaL, October 2023