Problem A. 864. (November 2023)

A. 864. Let \(\displaystyle ABC\) be a triangle and \(\displaystyle O\) be its circumcenter. Let \(\displaystyle D\), \(\displaystyle E\) and \(\displaystyle F\) be the respective tangent points of the incircle of \(\displaystyle \triangle ABC\), and sides \(\displaystyle BC\), \(\displaystyle CA\) and \(\displaystyle AB\). Let \(\displaystyle M\) and \(\displaystyle N\) be the respective midpoints of sides \(\displaystyle AB\) and \(\displaystyle AC\). Let \(\displaystyle M'\) and \(\displaystyle N'\) be the respective reflections of points \(\displaystyle M\) and \(\displaystyle N\) across lines \(\displaystyle DE\) and \(\displaystyle DF\). Let lines \(\displaystyle CM'\) and \(\displaystyle BN'\) intersect lines \(\displaystyle DE\) and \(\displaystyle DF\) at points \(\displaystyle H\) and \(\displaystyle J\), respectively.

Prove that the points \(\displaystyle H\), \(\displaystyle J\) and \(\displaystyle O\) are collinear.

Proposed by Luu Dong, Vietnam

(7 pont)

Deadline expired on December 11, 2023.

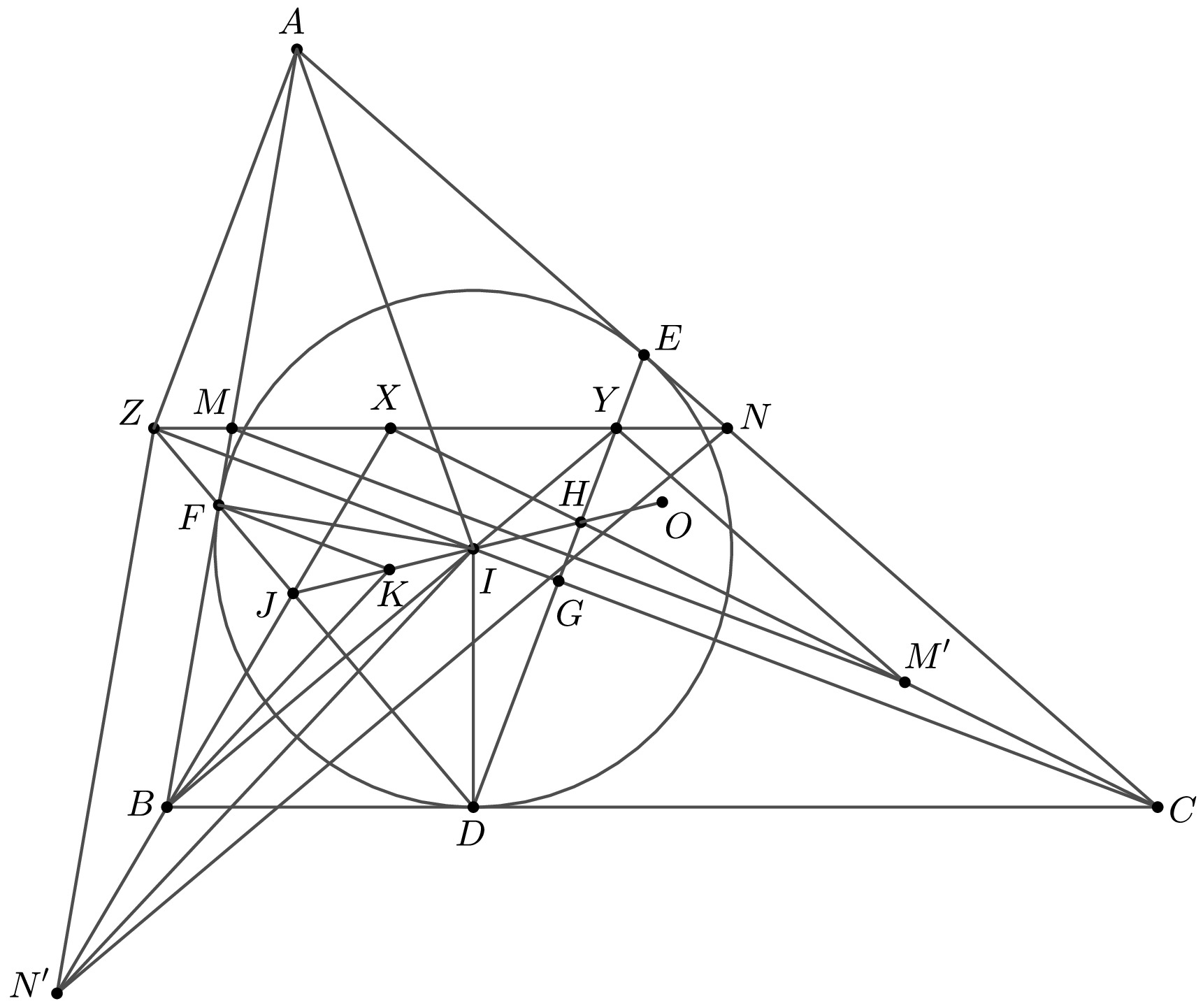
Denote by \(\displaystyle I\) the center of the circle \(\displaystyle (DEF)\). Let \(\displaystyle X\) be the intersection of the lines \(\displaystyle MN\) and \(\displaystyle CH\). Let \(\displaystyle Y \) be the intersection of the lines \(\displaystyle BI \) and \(\displaystyle DE\); \(\displaystyle Z\) is the intersection of the lines \(\displaystyle CI\) and \(\displaystyle DF\). Denote by \(\displaystyle K\) the orthocenter of triangle \(\displaystyle DEF\). Finally, let \(\displaystyle G\) be the midpoint of \(\displaystyle DE\). We use the usual \(\displaystyle \alpha\), \(\displaystyle \beta\), \(\displaystyle \gamma\) notations for the angles of triangle \(\displaystyle ABC\).

We start the proof with three well-known lemmas and sketches of their proof.

Lemma 1: Point \(\displaystyle Z\) lies on \(\displaystyle MN\) and \(\displaystyle \angle AZC=90^\circ\).

Proof sketch: By angle chasing \(\displaystyle \frac{\alpha}{2}=\angle FZI=\angle FAI\), hence \(\displaystyle A, Z, F, I\) lie on a circle. This implies that \(\displaystyle \angle AZC=\angle AFI=90^\circ\). Hence \(\displaystyle N\) is the midpoint of circle \(\displaystyle (AZC)\), so \(\displaystyle \angle CZN=\angle NCZ=\angle ZCB\), thus \(\displaystyle ZN \parallel BC\) meaning that \(\displaystyle M\) is on the line \(\displaystyle ZN\).

Lemma 2: \(\displaystyle K\), \(\displaystyle I\) and \(\displaystyle O\) are collinear.

Proof sketch: Let \(\displaystyle A'\), \(\displaystyle B'\), \(\displaystyle C'\) be the excenters of triangle \(\displaystyle ABC\). The sides of \(\displaystyle A'B'C'\) are parallel to the sides of \(\displaystyle DEF\), hence there exists a homothety that transforms \(\displaystyle A'B'C'\) to \(\displaystyle DEF\). This implies that the Euler-lines of the two triangle are parallel. Note that \(\displaystyle I\) is the circumcenter and \(\displaystyle K\) is the orthocenter of \(\displaystyle DEF\), hence \(\displaystyle IK\) is the Euler-line of \(\displaystyle DEF\). Furthermore, \(\displaystyle I\) is the orthocenter and \(\displaystyle O\) is the nine-point center of \(\displaystyle A'B'C'\), hence \(\displaystyle IO\) is the Euler-line of \(\displaystyle A'B'C'\). The conclusion follows.

Lemma 3: \(\displaystyle 2 \cdot IG=FK\)

Proof sketch: Remember that \(\displaystyle K\) is the orthocenter and \(\displaystyle I\) is the circumcenter of \(\displaystyle DEF\). By angle chasing, the reflection \(\displaystyle K'\) of \(\displaystyle K\) through \(\displaystyle G\) lies on the circle \(\displaystyle (DEF)\), furthermore this is the point opposite to \(\displaystyle F\) in this circle. Consequently, \(\displaystyle IG\) is the midline of triangle \(\displaystyle FKK'\), which proves the lemma.

Notice that by symmetry, \(\displaystyle Y\) also belongs to line \(\displaystyle MN\) as \(\displaystyle Z\) (by Lemma 1). As \(\displaystyle CE=CD\), we have \(\displaystyle EN=YN\), hence

\(\displaystyle \angle DYM'=\angle DYM=\angle NYE=\angle YEN.\)

This means \(\displaystyle YM'\parallel EC\). Similarly, \(\displaystyle ZN'\parallel FB\). It is easy to see that \(\displaystyle MM'\parallel CZ\), hence

\(\displaystyle \dfrac{YX}{YN} = \dfrac{M'X}{M'C} =\dfrac{MX}{MZ} .\)

Notice that if \(\displaystyle X'\) is the intersection of \(\displaystyle N'B\) and \(\displaystyle MN\) then a similar calculation shows

\(\displaystyle \dfrac{YX'}{YN}=\dfrac{MX'}{MZ}\)

implying \(\displaystyle X=X'\), hence \(\displaystyle N'\), \(\displaystyle B\) and \(\displaystyle X\) are collinear. Applying Pappus's theorem to six points \(\displaystyle Z, X, Y, B, D\) and \(\displaystyle C\) we get that points \(\displaystyle BX\cap DZ = J, \ CX\cap DY = H, \ BY\cap CZ = I\) are collinear.

By angle chasing, \(\displaystyle \angle AIZ=\angle FIB=90^\circ-\frac{\beta}{2}\). Combining this with Lemma 1, the triangles \(\displaystyle AZI\) and \(\displaystyle BFI\) are similar, hence \(\displaystyle ZI\cdot BF = AZ\cdot IF\). Using Lemma 1, \(\displaystyle AZ=AC\cdot \sin \dfrac{\gamma}{2}\). Clearly, \(\displaystyle \angle IDG=\frac{\gamma}{2}\). Using Lemma 3 and Lemma 1 once more, we calculate

\(\displaystyle AZ\cdot IF = AC\cdot \sin \dfrac{\gamma}{2} \cdot ID= 2ZN \cdot \sin (\angle{IDG}) \cdot ID= 2ZN'\cdot IG =ZN'\cdot FK.\)

It follows that \(\displaystyle ZI\cdot BF = ZN'\cdot FK.\) We get

\(\displaystyle \dfrac{FK}{ZI}=\dfrac{BF}{ZN'}=\dfrac{JF}{JZ}.\)

This implies that the points \(\displaystyle J, K\) and \(\displaystyle I\) are collinear. We proved earlier that \(\displaystyle J, H\) and \(\displaystyle I\) are collinear and by Lemma 2, \(\displaystyle K, I\) and \(\displaystyle O\) are collinear. Combining these, \(\displaystyle J, K, I, H, O\) are collinear, which finishes the proof.

Statistics:

15 students sent a solution.
7 points:	Bodor Mátyás, Czanik Pál, Diaconescu Tashi, Philip Stefanov, Simon László Bence, Tianyue DAI, Varga Boldizsár, Virág Rudolf, Wiener Anna.
3 points:	1 student.
2 points:	1 student.
1 point:	1 student.
0 point:	3 students.

Problems in Mathematics of KöMaL, November 2023