Problem A. 868. (December 2023)

A. 868. A set of points in the plane is called disharmonic, if the ratio of any two distances between the points is between \(\displaystyle 100/101\) and \(\displaystyle 101/100\), or at least 100 or at most \(\displaystyle 1/100\).

Is it true that for any distinct points \(\displaystyle A_1, A_2,\ldots, A_n\) in the plane it is always possible to find distinct points \(\displaystyle A'_1, A'_2,\ldots,A'_n\) that form a disharmonic set of points, and moreover \(\displaystyle A_i\), \(\displaystyle A_j\) and \(\displaystyle A_k\) are collinear in this order if and only if \(\displaystyle A'_i\), \(\displaystyle A'_j\) and \(\displaystyle A'_k\) are collinear in this order (for all distinct \(\displaystyle 1\le i,j,k\le n\))?

Submitted by Dömötör Pálvölgyi and Balázs Keszegh, Budapest

(7 pont)

Deadline expired on January 10, 2024.

The statement is not true.

The main idea is that we consider a set of points with so many incidences that all transformations preserving incidence will also be projective, thus preserving cross-ratios. We will show that disharmonic set of points cannot contain harmonic quadraples, while the original set of points can.

Lemma: if \(\displaystyle D\), \(\displaystyle A\), \(\displaystyle C\) and \(\displaystyle B\) are four distinct collinear points of a disharmonic set of points in this order, then \(\displaystyle (A;B;C;D)\) cannot be -1, therefore it cannot be harmonic.

Proof: Suppose for the sake of contradiction that this is not true. Let \(\displaystyle DA=a\), \(\displaystyle AC=b\), \(\displaystyle CB=c\) (with \(\displaystyle a,b,c>0\)). The condition for being harmonic is \(\displaystyle AC/CB=DA/DB\), i.e. \(\displaystyle ac=a(a+b+c)\). This implies \(\displaystyle b\le a\) and \(\displaystyle b\le c\), and the role of \(\displaystyle a\) and \(\displaystyle c\) is symmetric, therefore we can assume \(\displaystyle b\le a\le c\). If \(\displaystyle a\le 1.01 b\), then \(\displaystyle 2\le (a+b)/b\le 2.01\), which is not allowed in a disharmonic set of points. Thus \(\displaystyle 100b\le a\le c\). Let \(\displaystyle a=xb\) and \(\displaystyle c=yb\) where \(\displaystyle 100\le x\le y\). Substituting this into the equality and dividing by \(\displaystyle b^2\) we get \(\displaystyle xy=x+y+1\). But this is clearly impossible, since \(\displaystyle x+y+1<100y\le xy\). This is a contradiction, so the statement of the lemma is true.

Consider the following figure: we start with convex quadrilateral \(\displaystyle ABCD\). \(\displaystyle E\) is the intersection point of lines \(\displaystyle AB\) and \(\displaystyle CD\), \(\displaystyle F\) is the intersection point of lines \(\displaystyle AD\) and \(\displaystyle BC\), \(\displaystyle G\) is the intersection of diagonals \(\displaystyle AC\) and \(\displaystyle BD\). Finally, let \(\displaystyle H\), \(\displaystyle I\), \(\displaystyle J\) and \(\displaystyle K\) be the intersection points of lines \(\displaystyle EG\) and \(\displaystyle AD\), \(\displaystyle FG\) and \(\displaystyle AB\), \(\displaystyle EG\) and \(\displaystyle BC\) and \(\displaystyle FG\) and \(\displaystyle CD\), respectively.

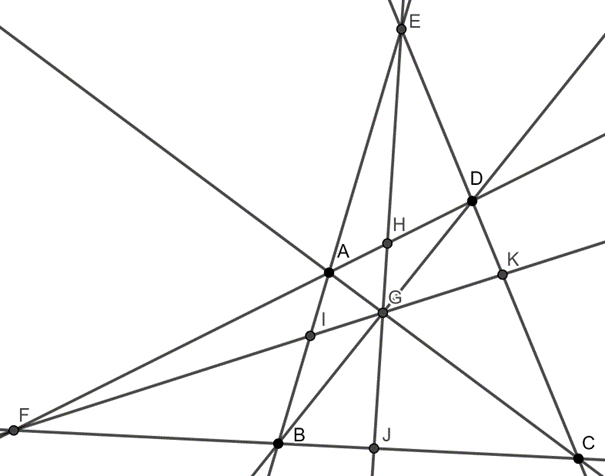
We claim that for these 11 points we cannot find a disharmonic set of points.

Let's assume for the sake of contradiction that there exists a disharmonic set of points for this configuration, and let point \(\displaystyle X\) be mapped to point \(\displaystyle X'\). According to the conditions, \(\displaystyle A'B'C'D'\) is also a quadrilateral, and the remaining points can be obtained using the above method, for example \(\displaystyle E'\) has to be the intersection of lines \(\displaystyle A'B'\) and \(\displaystyle C'D'\), \(\displaystyle F'\) has to be the intersection of lines \(\displaystyle A'D'\) and \(\displaystyle B'C'\), and so on.

It is well known that points \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) and \(\displaystyle D\) can be mapped to \(\displaystyle A'\), \(\displaystyle B'\), \(\displaystyle C'\) and \(\displaystyle D'\) using a projective transformation. The projective transformations preserve incidence, and thus the rest of points has to mapped to the corresponding point in the disharmonic configuration (thus \(\displaystyle E\) to \(\displaystyle E'\), \(\displaystyle F\) to \(\displaystyle F'\), and so on). It is well known that \(\displaystyle (E';G';H';J')\) is a harmonic quadraple (an easy way to show this is two project \(\displaystyle A'B'C'D'\) into a parallelogram), but this contradicts our lemma.

Statistics:

6 students sent a solution.
7 points:	Varga Boldizsár, Wiener Anna.
0 point:	4 students.

Problems in Mathematics of KöMaL, December 2023