 Problem A. 871. (January 2024)
Problem A. 871. (January 2024)
A. 871. Let \(\displaystyle ABC\) be an obtuse triangle, and let \(\displaystyle H\) denote its orthocenter. Let \(\displaystyle \omega_A\) denote the circle with center \(\displaystyle A\) and radius \(\displaystyle AH\). Let \(\displaystyle \omega_B\) and \(\displaystyle \omega_C\) be defined in a similar way. For all points \(\displaystyle X\) in the plane of triangle \(\displaystyle ABC\) let circle \(\displaystyle \Omega(X)\) be defined in the following way (if possible): take the polars of point \(\displaystyle X\) with respect to circles \(\displaystyle \omega_A\), \(\displaystyle \omega_B\) and \(\displaystyle \omega_C\), and let \(\displaystyle \Omega(X)\) be the circumcircle of the triangle defined by these three lines.
With a possible exception of finitely many points find the locus of points \(\displaystyle X\) for which point \(\displaystyle X\) lies on circle \(\displaystyle \Omega(X)\).
Proposed by Vilmos Molnár-Szabó, Budapest
(7 pont)
Deadline expired on February 12, 2024.
Let \(\displaystyle X_A\), \(\displaystyle X_B\) and \(\displaystyle X_C\) denote the inverse image of \(\displaystyle X\) with respect to circles \(\displaystyle \omega_A\), \(\displaystyle omega_B\) and \(\displaystyle omega_C\). Let \(\displaystyle A'\), \(\displaystyle B'\) and \(\displaystyle C'\)be the reflection of orthocenter \(\displaystyle H\) across sides \(\displaystyle BC\), \(\displaystyle AC\) and \(\displaystyle AB\) (it's well known, that these are on the circumcircle of \(\displaystyle ABC\)). Observe that \(\displaystyle A'\) is on \(\displaystyle \omega_B\) and \(\displaystyle \omega_C\), since \(\displaystyle H\) is one of their intersections, and the line connecting their centers is \(\displaystyle BC\). Our first claim is that the circumcircle of triange \(\displaystyle XX_AX_B\) is the Apollonius circle of line segment \(\displaystyle HC'\).
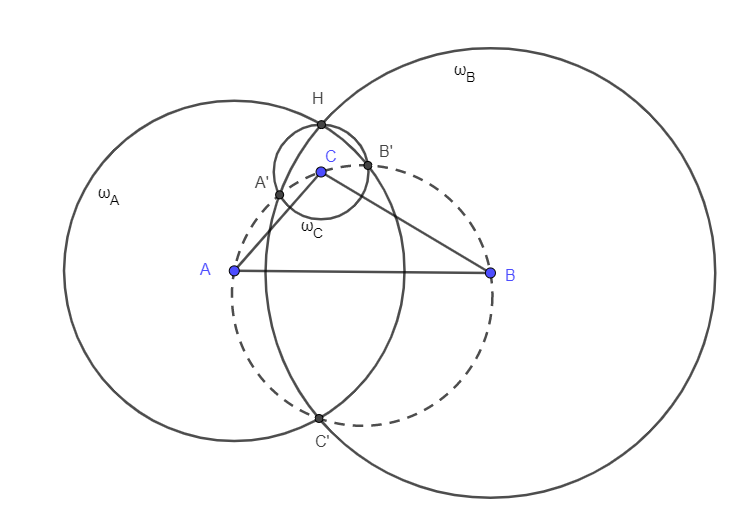
We will use the well known statement that the fixed circle of an inversion is the Apollonius circle of a point and its inverse image. This implies that \(\displaystyle \omega_A\) and \(\displaystyle \omega_B\) are the Apollonius circles line segments \(\displaystyle XX_A\) and \(\displaystyle XX_B\), respectively. The intersections of these circles are \(\displaystyle H\) and \(\displaystyle C'\), therefore \(\displaystyle HX/HX_A=C'X/C'X_A\) and \(\displaystyle HX/HX_B=C'X/C'X_B\). Rearranging these leads to \(\displaystyle HX/C'X=HX_A/C'X_A=HX_B/C'X_B\), therefore \(\displaystyle X\), \(\displaystyle X_A\) and \(\displaystyle X_B\) are on the Apollonius circle of \(\displaystyle HC'\), as we claimed. Let \(\displaystyle O_A\) denote the center of this circle, and let \(\displaystyle O_B\) and \(\displaystyle O_C\) be defined similarly.
Now let's consider an inversion with center \(\displaystyle H\) which maps \(\displaystyle A\) to \(\displaystyle A'\), \(\displaystyle B\) to \(\displaystyle B'\) and \(\displaystyle C\) to \(\displaystyle C'\). Such an inversion always exists if we allow circles with imaginary radius, however, an actual circle exists exactly if \(\displaystyle H\) lies outside of the circumcircle of \(\displaystyle ABC\), i.e. if \(\displaystyle ABC\) is obtuse. In this case, let \(\displaystyle k\) denote the fixed circle of the inversion, and let \(\displaystyle X'\) denote the inverse image of \(\displaystyle X\) with respect to \(\displaystyle k\).
It's well known that the polar of \(\displaystyle X\) with respect to \(\displaystyle \omega_A\) is the perpendicular to \(\displaystyle XH\) at point \(\displaystyle X_A\). A similar claim is true for \(\displaystyle \omega_B\), therefore the intersection of the two polars is the point that is opposite from \(\displaystyle X\) on circle \(\displaystyle XX_AX_B\). If we apply a homothety from point \(\displaystyle X\) with ratio \(\displaystyle 1/2\), the image of this intersection becomes \(\displaystyle O_C\), and thus the condition of the problem transforms to \(\displaystyle X\), \(\displaystyle O_A\), \(\displaystyle O_B\) and \(\displaystyle O_C\) being concyclic. Using directed angles mod \(\displaystyle 180^{\circ}\), the condition becomes equivalent to \(\displaystyle \angle O_CXO_B=\angle O_CO_AO_B\). Let's take a closer look at these angles.
Note that \(\displaystyle O_AO_C\) is perpendicular to \(\displaystyle XB\): circles \(\displaystyle XX_BX_C\) and \(\displaystyle XX_AX_B\) intersect at at points \(\displaystyle X\) and \(\displaystyle X_B\), therefore \(\displaystyle XX_B\) in perpendicular to line \(\displaystyle O_AO_C\) connecting the centers of these circles, and \(\displaystyle X\), \(\displaystyle X_B\) and \(\displaystyle B\) are collinear, since \(\displaystyle X_B\) is the inverse image \(\displaystyle X\) with respect to \(\displaystyle \omega_B\), the center of which is \(\displaystyle B\). Similarly, \(\displaystyle O_AO_B\) and \(\displaystyle XC\) are also perpendicular, therefore \(\displaystyle \angle O_CO_AO_B = \angle BXC\) (we will keep using directed angles mod \(\displaystyle 180^{\circ}\)).
Now let's focus on angle \(\displaystyle \angle O_CXO_B\): let's rewrite it as the difference \(\displaystyle \angle O_CXO_B = \angle HXO_B - \angle HXO_C\). Determining angle \(\displaystyle \angle HXO_B\) is based on our previous claim: circle \(\displaystyle XX_AX_C\) is the Apollonius circle of \(\displaystyle HB'\), the center of which is \(\displaystyle O_B\), and then \(\displaystyle \angle HXO_B = \angle O_BB'X = \angle HB'X\) (see the figure below).
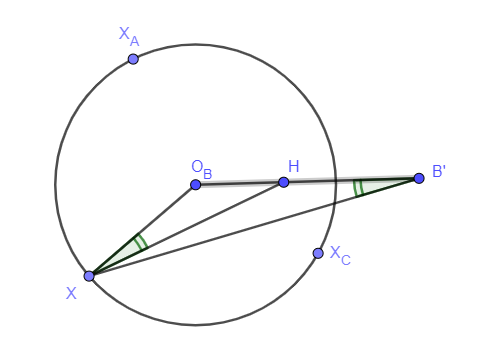
Finally, considering the inversion with respect to circle \(\displaystyle k\) we get that \(\displaystyle \angle HB'X = \angle HX'B\), since \(\displaystyle B\) and \(\displaystyle B'\) are also the inverse image of each other with respect to \(\displaystyle k\). So finally we get that \(\displaystyle \angle O_CXO_B = \angle HXO_B - \angle HXO_C = \angle HB'X - \angle HC'X = - \angle HX'B + \angle HX'C = \angle BX'C\).
Therefore, the condition in the problem is equivalent to \(\displaystyle \angle BXC = \angle BX'C\), and this is equivalent to \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle X\) and \(\displaystyle X'\) being concyclic. This happens when \(\displaystyle X = X'\), i.e. if \(\displaystyle X\) is on \(\displaystyle k\). Supposing \(\displaystyle X \neq X'\) implies that this circle is the circle passing through \(\displaystyle B\) and \(\displaystyle C\) and perpendicular to \(\displaystyle k\), which is the circumcircle of triangle \(\displaystyle ABC\).
We have answered the question in the problem: the locus of the points \(\displaystyle X\) satisfying the conditions of the problem are \(\displaystyle k\) and the circumcircle of triangle \(\displaystyle ABC\). Note that the argument works for acute triangles, too, however, in this case \(\displaystyle k\) does not exist (the imaginary inversion has no fixes points), therefore the answer in this case restricts to just the circumcircle.
Remark: If we invert with respect to \(\displaystyle k\), the image of circle \(\displaystyle \omega_A\) becomes line \(\displaystyle BC\), and thus the inversion across \(\displaystyle omega_A\) becomes reflection across \(\displaystyle BC\). By Simson's theorem the condition of the problem is equivalent to \(\displaystyle X_A\), \(\displaystyle X_B\) and \(\displaystyle X_C\) being collinear, and after the inversion with respect to \(\displaystyle k\) this condition becomes that the reflections of \(\displaystyle X'\) across the sides of triangle \(\displaystyle ABC\) and \(\displaystyle H\) is concyclic or collinear. Then we qucikly get the the circumcircle of \(\displaystyle ABC\) will work, since reflecting its points across the sides will result in a line passing through \(\displaystyle H\). Therefore \(\displaystyle X'\) being on the circumcircle works, but since the circumcircle is invariant at the inversion with respect to \(\displaystyle k\), this is equivalent to \(\displaystyle X\) being on the circumcircle, too.
Statistics:
7 students sent a solution. 7 points: Bodor Mátyás, Varga Boldizsár, Wiener Anna. 6 points: Foris Dávid. 5 points: 1 student. 3 points: 2 students.
Problems in Mathematics of KöMaL, January 2024
