Problem A. 873. (February 2024)

A. 873. Let \(\displaystyle ABCD\) be a convex cyclic quadrilateral satisfying \(\displaystyle AB\cdot CD=AD\cdot BC\). Let the inscribed circle \(\displaystyle \omega\) of triangle \(\displaystyle ABC\) be tangent to sides \(\displaystyle BC\), \(\displaystyle CA\) and \(\displaystyle AB\) at points \(\displaystyle A'\), \(\displaystyle B'\) and \(\displaystyle C'\), respectively. Let point \(\displaystyle K\) be the intersection of line \(\displaystyle ID\) and the nine-point-circle of triangle \(\displaystyle A'B'C'\) that is inside line segment \(\displaystyle ID\). Let \(\displaystyle S\) denote the centroid of triangle \(\displaystyle A'B'C'\). Prove that lines \(\displaystyle SK\) and \(\displaystyle BB'\) intersect each other on circle \(\displaystyle \omega\).

Proposed by Áron Bán-Szabó, Budapest

(7 pont)

Deadline expired on March 11, 2024.

Those \(\displaystyle ABCD\) cyclic quadrilaterals, in which \(\displaystyle AB\cdot CD = BC \cdot DA\) are called harmonic. The most important geometric property of a harmonic quadrilateral is the following: a cyclic quadrilateral is harmonic if and only if the tangents at two opposite vertices of the quadrilateral meet on the the other diagonal, or both tangents and the other diagonal are parallel.

This well known claim can be proved using the tangent-chord theorem: if the tangents at \(\displaystyle A\) and \(\displaystyle C\) meet at \(\displaystyle T\) on diagonal \(\displaystyle BD\), then triangles \(\displaystyle DAT\) and \(\displaystyle ABT\) are similar, therefore \(\displaystyle DA/AB=AT/BT\), and similarly we get \(\displaystyle CD/BC=CT/BT\). Since \(\displaystyle CT=AT\) due to the tangent segment theorem, we get \(\displaystyle DA/AB=CD/BC\) and this rearranges to the condition in the beginning. To prove the reverse direction, we apply the earlier case to \(\displaystyle ABCD'\), where \(\displaystyle D'\) is the point where the circle and line \(\displaystyle BT\) meet.

(If \(\displaystyle BD\) and the two tangents are parallel, \(\displaystyle ABCD\) is a kite, which satisfies the harmonic condition.)

We will also use the fact that the inverse image of a harmonic quadrilateral is also harmonic. Since inversion preserves the cross ratio, and similar to the line, the cross ratio \(\displaystyle (A,C,B,D)\) on a circle is also defined with the formula \(\displaystyle AB/BC\cdot DB/AD\) (with the appropriate sign: it is negative if and only if chords \(\displaystyle AC\) and \(\displaystyle BD\) intersect each other), the statement is clearly true. This fact about the cross ration can actually be proved easily: if the image of \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) and \(\displaystyle D\) is \(\displaystyle A'\), \(\displaystyle B'\), \(\displaystyle C'\) and \(\displaystyle D'\), and the center of the inversion is \(\displaystyle O\), then it is well known that \(\displaystyle AB/A'B'=OA/OB'\), and thus \(\displaystyle A'B'/B'C'=AB/BC\cdot OB'/OA\cdot OC/OB'=AB/BC\cdot OC/CA\), and the same holds for replacing \(\displaystyle B\) with \(\displaystyle D\), which implies the statement.

Now we solve the problem.

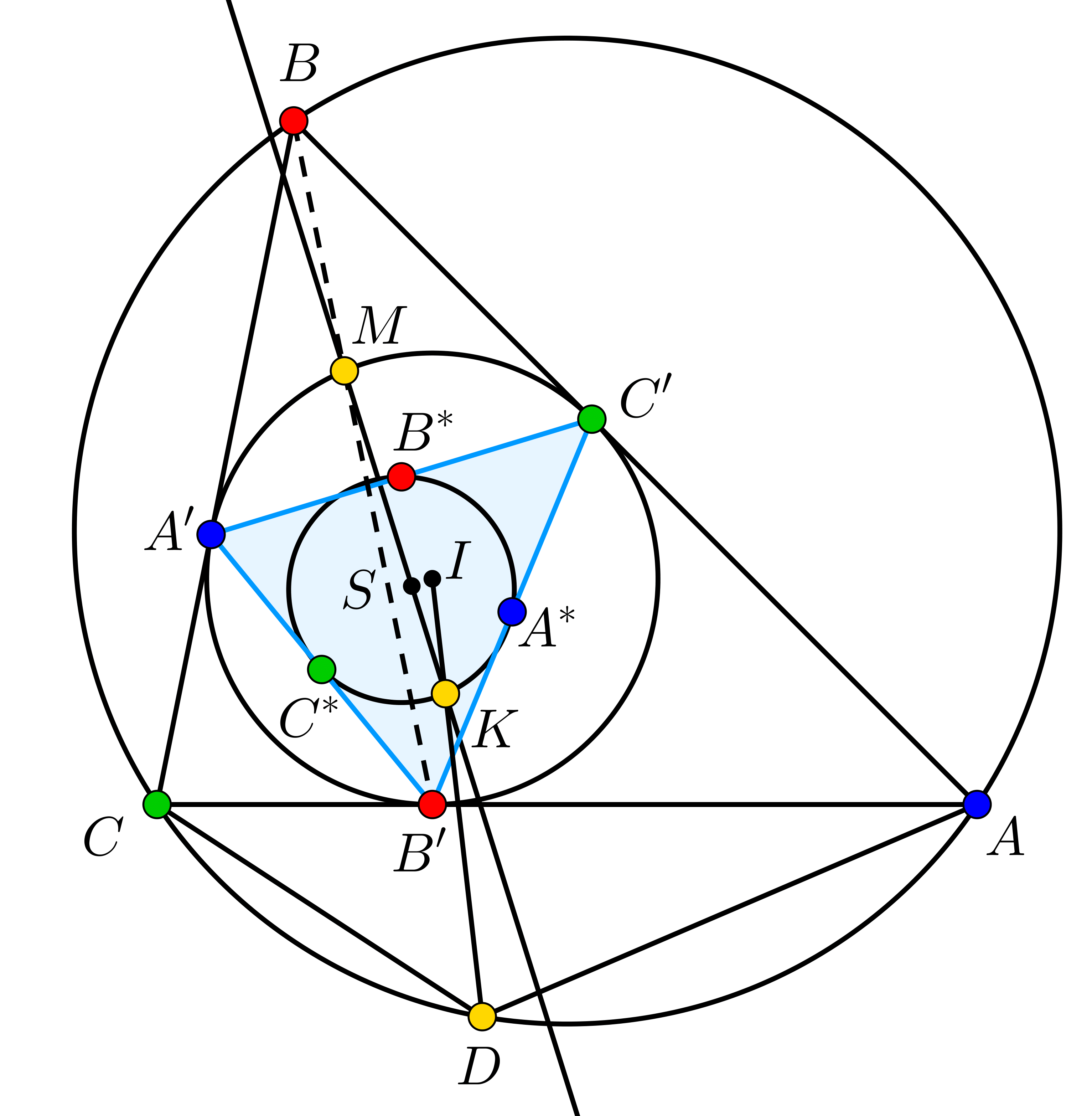
Let's invert with respect to the inscribed circle. The image of \(\displaystyle A\) is the midpoint of \(\displaystyle B'C'\), denoted by \(\displaystyle A^*\) (this is an easy to check basic property of inversion), and similar is true for \(\displaystyle B\) and \(\displaystyle C\). Therefore the image of circle \(\displaystyle (ABC)\) is the nine-point circle of \(\displaystyle A'B'C'\). The inverse image if \(\displaystyle D\) must be on ray \(\displaystyle ID\), and also on this nine-point circle, therefore it must be point \(\displaystyle K\) from the problem.

Now let's apply a homothety from centroid \(\displaystyle S\) of \(\displaystyle A'B'C'\) with a ratio of \(\displaystyle -2\): it maps \(\displaystyle A^*\) to \(\displaystyle A'\), and similar is true for \(\displaystyle B\) and \(\displaystyle C\). Let \(\displaystyle M\) denote the imgae of \(\displaystyle K\). Then \(\displaystyle M\) must be on the incribed circle, \(\displaystyle \omega\), and we have seen that \(\displaystyle A'B'C'M\) must be harmonic (since \(\displaystyle ABCD\) was harmonic, and both the inversion and the homothety preserve harmonic quadrilaterals). Therefore, diagonal \(\displaystyle B'M\) must go through the tangents of \(\displaystyle \omega\) at \(\displaystyle A'\) and \(\displaystyle C'\) (i.e. \(\displaystyle BC\) and \(\displaystyle BA\)), which is exactly point \(\displaystyle B\), and this was to be proved.

Statistics:

14 students sent a solution.
7 points:	Bodor Mátyás, Chrobák Gergő, Czanik Pál, Diaconescu Tashi, Foris Dávid, Holló Martin, Nguyen Kim Dorka, Philip Stefanov, Simon László Bence, Szakács Ábel, Varga Boldizsár, Virág Rudolf, Wiener Anna.
6 points:	Forrai Boldizsár.

Problems in Mathematics of KöMaL, February 2024