 Problem A. 875. (March 2024)
Problem A. 875. (March 2024)
A. 875. \(\displaystyle a)\) Two players play a cooperative game. They can discuss a strategy prior to the game, however, they cannot communicate and have no information about the other player during the game. The game master chooses one of the players in each round. The player on turn has to guess the number of the current round. Players keep note of the number of rounds they were chosen, however, they have no information about the other player's rounds. If the player's guess is correct, the players are awarded a point. Player's are not notified whether they've scored or not. The players win the game upon collecting 100 points. Does there exist a strategy with which they can surely win the game in a finite number of rounds?
\(\displaystyle b)\) How does this game change, if in each round the player on turn has two guesses instead of one, and they are awarded a point if one of the guesses is correct (while keeping all the other rules of the game the same)?
Proposed by Gábor Szűcs, Budapest
(7 pont)
Deadline expired on April 10, 2024.
a) Let the two players be \(\displaystyle A\) and \(\displaystyle B\). One point can always be achieved, for instance, if both players guess \(\displaystyle 1\) every round. However, more than that is not guaranteed: Let \(\displaystyle a_k\) denote Player \(\displaystyle A\)'s guess in the \(\displaystyle k\)-th round, and similarly define the sequence \(\displaystyle b_k\) for Player \(\displaystyle B\)'s guesses.
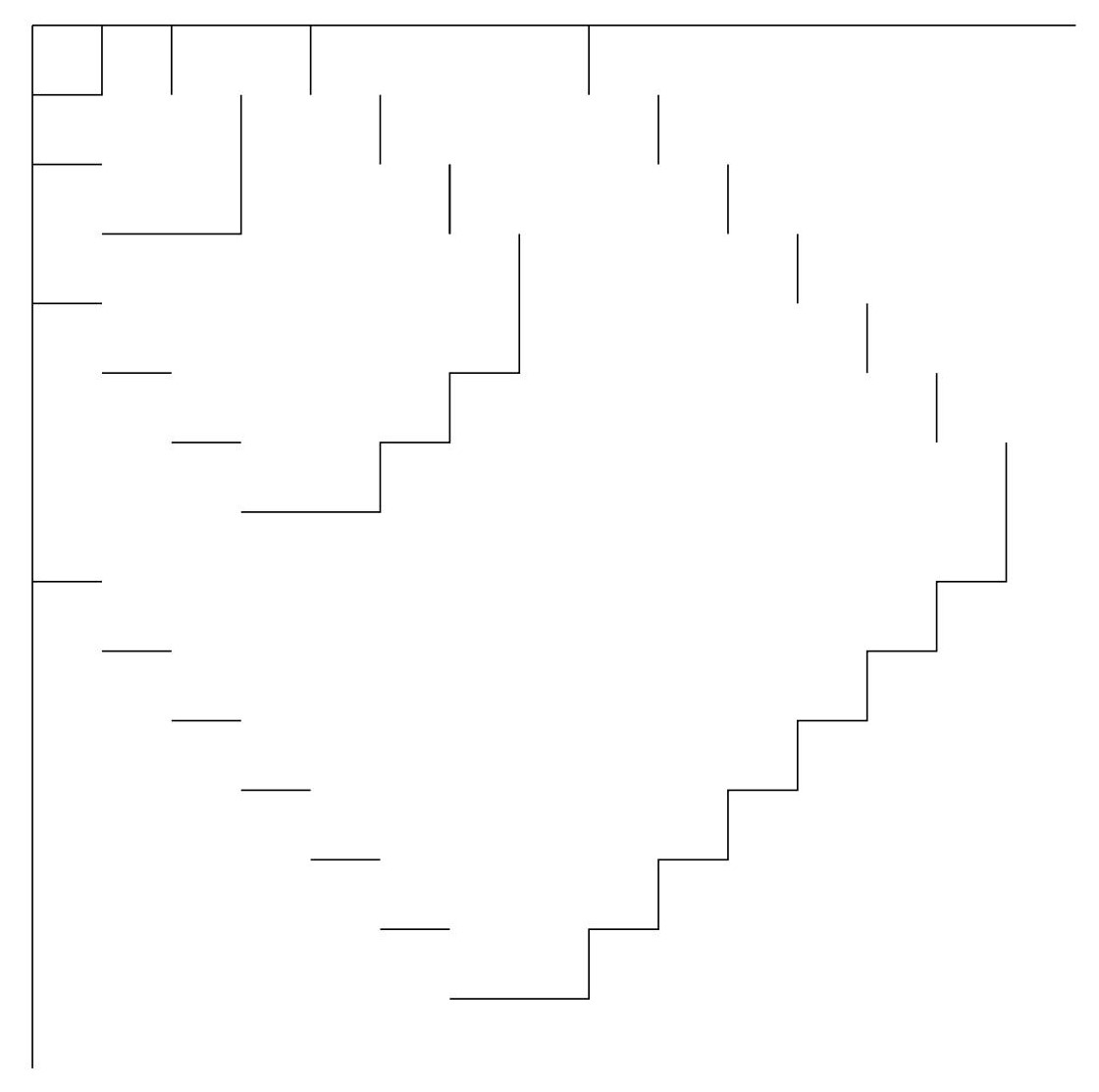
We will illustrate the progress of the game in a table consisting of unit squares in the fourth quadrant as follows: We start from the top-left corner (indexed as \(\displaystyle (0,0)\)) and move rightward if Player \(\displaystyle A\) is called in that round, otherwise downward. Additionally, let's place vertical and horizontal walls in the table, the former on the right side of squares with coordinates \(\displaystyle (k-1,-(a_k-k))\), and the latter at the bottom of squares with coordinates \(\displaystyle (-(b_k-k),k-1)\).
Consider the game in this representation: initially, the players can place at most one wall on the right edge of every vertical column and on the bottom edge of every horizontal row. Then, in each step, we move one unit to the right or downward (determined by the game master), and if we cross a vertical or horizontal wall, the players earn a point. When the game master has called \(\displaystyle A\) for \(\displaystyle n\) times and \(\displaystyle B\) for \(\displaystyle m\) times, and now calls \(\displaystyle A\) again, the players earn a point if \(\displaystyle a_{n+1}=n+m+1\). This corresponds to moving from square \(\displaystyle (n,-m)\) to square \(\displaystyle (n+1,-m)\), hence crossing a wall, if and only if \(\displaystyle -(a_{n+1}-(n+1))=-m\), which is equivalent to \(\displaystyle a_{n+1}=n+m+1\).
The players aim to place walls such that regardless of the movement chosen by the game master, they will hit at least \(\displaystyle 100\) walls within a finite number of steps.
Suppose that the players have somehow placed walls according to the rules. Now, let the game master play as follows: until the players score a point, always move arbitrarily such that if possible, no point is scored for the players. The players can only earn their first point if they reach a square with walls on its bottom and right sides. Move rightward in this case. Afterward, keep moving right until reaching a wall. If this never happens, it's clear the players won't score more points. Once reaching a wall, since there was already a wall at the bottom of this row during a previous round (when the players scored), they won't score a point by moving downward. Then, move downward until reaching another wall. Again, it will be true that there was a wall at the right edge of the column, allowing us to move rightward. Repeat this process, alternately moving rightward or downward until encountering a wall, thus ensuring the players can never score more than one point.
b) Prepare a table similar to the one described above. The only difference from part a) is that now, each row's bottom edge and each column's right edge can accommodate two walls. In this case, the players can win using the following construction (which can be continued indefinitely according to this pattern). The game master is forced to intersect a wall in every layer, ensuring the players score \(\displaystyle 100\) points within a finite number of steps.
Statistics:
Problem A. 875. is not processed yet.
Problems in Mathematics of KöMaL, March 2024
