Problem A. 885. (September 2024)

A. 885. Let triangle \(\displaystyle ABC\) be a given acute scalene triangle with altitudes \(\displaystyle BE\) and \(\displaystyle CF\). Let \(\displaystyle D\) be the point where the incircle of \(\displaystyle \triangle ABC\) touches side \(\displaystyle B C\). The circumcircle of \(\displaystyle \triangle B D E\) meets line \(\displaystyle A B\) again at point \(\displaystyle K\), the circumcircle of \(\displaystyle \triangle C D F\) meets line \(\displaystyle A C\) again at point \(\displaystyle L\). The circumcircle of \(\displaystyle \triangle B D E\) and \(\displaystyle \triangle CDF\) meet line \(\displaystyle KL\) again at \(\displaystyle X\) and \(\displaystyle Y\), respectively. Prove that the incenter of \(\displaystyle \triangle DXY\) lies on the incircle of \(\displaystyle \triangle ABC\).

Proposed by Luu Dong, Vietnam

(7 pont)

Deadline expired on October 10, 2024.

Let \(\displaystyle (I)\) be the incircle of \(\displaystyle \triangle ABC.\) Denote the intersection point of \(\displaystyle DI\) and \(\displaystyle AC, AB\) by \(\displaystyle P, Q\) respectively. Let \(\displaystyle M, N \) be the points at which \(\displaystyle (I)\) touches the side \(\displaystyle AB, AC\), respectively. \(\displaystyle CI\) meets circle \(\displaystyle (CDF)\) again at \(\displaystyle S\). Denote the incenter of triangle \(\displaystyle DXY\) by \(\displaystyle J\).

It is evident that points \(\displaystyle P, Q, K,L\) lie on a circle with diameter \(\displaystyle PQ\). It follows that

\(\displaystyle \angle(QF, QD)= \angle(QK, QP)=\angle(LK, LP)=\angle(LY, LC).\)

Thus \(\displaystyle DY\parallel CF\). Similarly, \(\displaystyle DX\parallel BE\).

Since \(\displaystyle CS\) is the bisector of \(\displaystyle \angle ACD\), we get \(\displaystyle YS\) is the bisector of \(\displaystyle \angle KYD\). It implies that \(\displaystyle S, J, Y\) are collinear. (1)

We have \(\displaystyle S, M, I, Q\) lie on the circle with diameter \(\displaystyle IQ\). That means

\(\displaystyle \angle(SM, SI)=\angle (QM, QI).\)

We deduce that

\(\displaystyle \angle(SM, SC)=\angle (QF, QD)=\angle(SY, SC).\)

Thus \(\displaystyle S, M, Y\) are collinear. (2)

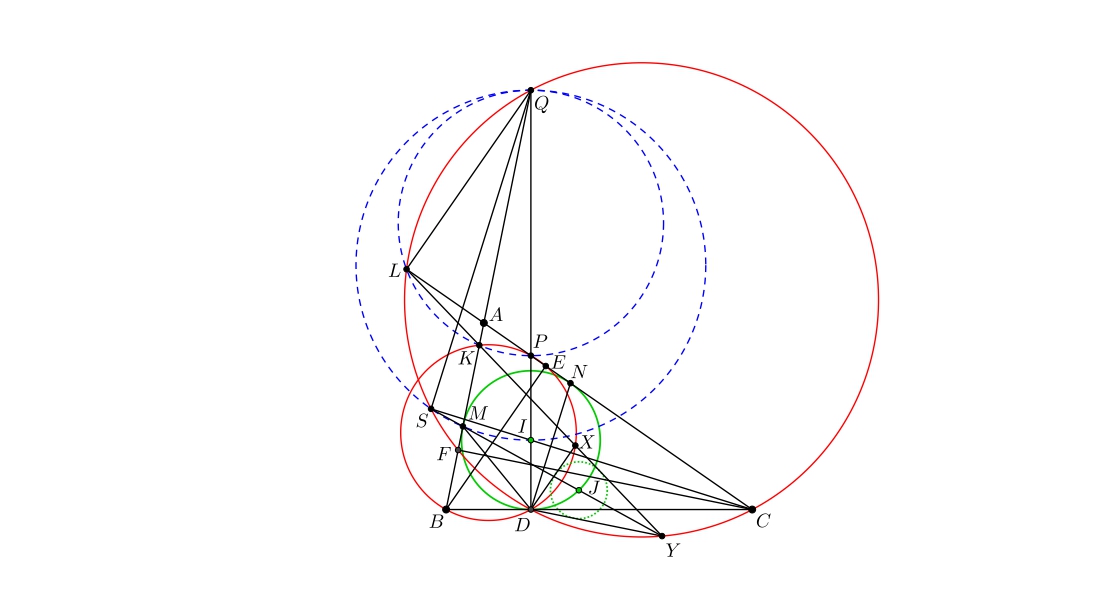
From (1) and (2) we get \(\displaystyle M, J, Y\) are collinear. Similarly, \(\displaystyle N, J, X\) are collinear. We have

\(\displaystyle \angle(XY, XD)=\angle(XK, XD)=\angle(BK, BD)=-\angle(BC, BA)\)

and similarly,

\(\displaystyle \angle(YX, YD)=-\angle(CB, CA).\)

It follows that the triangles \(\displaystyle DXY, ABC\) are similar. Thus triangles \(\displaystyle JXY, IBC\) are similar. We calculate

\(\displaystyle \angle(JM, JN)= \angle(JY, JX)=-\angle(IC, IB)=-\angle(DN, DM)=\angle(DM, DN).\)

Hence \(\displaystyle J, M, N, D\) are concyclic.

Statistics:

16 students sent a solution.
7 points:	Bodor Mátyás, Bui Thuy-Trang Nikolett, Czanik Pál, Diaconescu Tashi, Forrai Boldizsár, Holló Martin, Keresztély Zsófia, Lasitha Vishwajith Jayasinghe, Szakács Ábel, Tianyue DAI, Varga Boldizsár, Virág Lénárd Dániel, Virág Tóbiás.
3 points:	1 student.
0 point:	2 students.

Problems in Mathematics of KöMaL, September 2024