 Problem A. 891. (November 2024)
Problem A. 891. (November 2024)
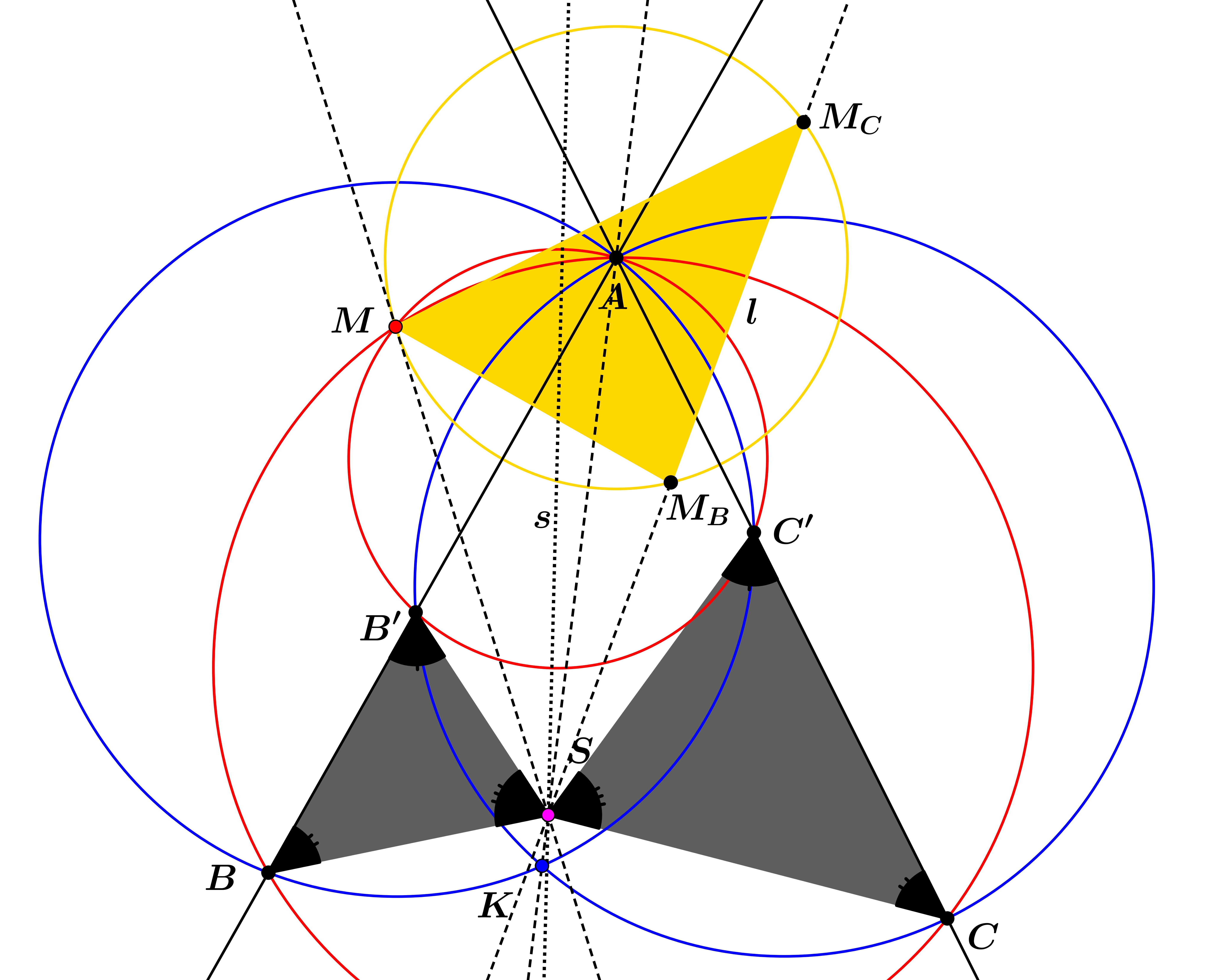
A. 891. Let \(\displaystyle ABC\) be an acute triangle. Points \(\displaystyle B'\) and \(\displaystyle C'\) are located on the interior of sides \(\displaystyle AB\) and \(\displaystyle AC\), respectively. Let \(\displaystyle M\) denote the second intersection of the circumcircles of triangles \(\displaystyle ABC\) and \(\displaystyle AB'C'\), while let \(\displaystyle N\) denote the second intersection of the circumcircles of triangles \(\displaystyle ABC'\) and \(\displaystyle AB'C\). Reflect \(\displaystyle M\) across lines \(\displaystyle AB\) and \(\displaystyle AC\), and let \(\displaystyle l\) denote the line through the reflections.
a) Prove that the line through \(\displaystyle M\) perpendicular to line \(\displaystyle AM\), the line \(\displaystyle AK\), and \(\displaystyle l\) are either concurrent or all parallel.
b) Show that if the three lines are concurrent at \(\displaystyle S\), then triangles \(\displaystyle SBC'\) and \(\displaystyle SCB'\) have equal areas.
Proposed by Áron Bán-Szabó, Budapest
(7 pont)
Deadline expired on December 10, 2024.
We will prove the second part of the problem first.
Denote by \(\displaystyle M_B,M_C\) the reflections of \(\displaystyle M\) in lines \(\displaystyle AB,AC\), respectively. Furthermore, define \(\displaystyle S\) as intersection of the line through \(\displaystyle M\) perpendicular to \(\displaystyle AM\) with \(\displaystyle l=M_BM_C\). Due to the reflections, we have \(\displaystyle AM=AM_B=AM_C\), so \(\displaystyle A \) is the circumcenter of triangle \(\displaystyle MM_BM_C\). It follows that \(\displaystyle SM\) is tangent to this circle (since \(\displaystyle \angle SMA=90^{\circ}\)). Thus, due to inscribed angles we have \(\displaystyle \angle SMM_B= \angle SM_CM\). Then, the angles of triangles \(\displaystyle SMM_B,SM_CM\) are pairwise equal, therefore they are similar, but clearly oppositely oriented. Consider a similarity transformation \(\displaystyle \mathcal{L}\) that sends triangle \(\displaystyle SMM_B\) to \(\displaystyle SM_CM\) and leaves \(\displaystyle S\) invariant. (Consider a reflection in the angel bisector of \(\displaystyle \angle MSM_B\) followed by a homothety with center \(\displaystyle S\) and ratio \(\displaystyle SM/SM_B\).) Thus, the similarity \(\displaystyle \mathcal{L}\) takes segment \(\displaystyle M_BM\) to segment \(\displaystyle MM_C\).
Now let us consider triangles \(\displaystyle BM_BM\) and \(\displaystyle CM_CM\). They are both isosceles as \(\displaystyle B\) and \(\displaystyle C\) lie on the perpendicular bisectors of segments \(\displaystyle MM_B,MM_C\), respectively. However, \(\displaystyle A\) lies on both perpendicular bisectors, thus by inscribed angles in circle \(\displaystyle MBCA\) we have \(\displaystyle \angle MBM_B=2 \angle MBA=2 \angle MCA= \angle MCM_C\). Therefore, \(\displaystyle \triangle BM_BM\sim\triangle CM_CM\). Since \(\displaystyle \mathcal{L}\) is a similarity sending segment \(\displaystyle M_BM\) to segment \(\displaystyle M_CM\), we conclude that it sends point \(\displaystyle B\) to \(\displaystyle C\). Applying the same argument to triangle \(\displaystyle AB'C'\) instead of triangle \(\displaystyle ABC\) we conclude that \(\displaystyle \mathcal{L}\) sends \(\displaystyle B’\) to \(\displaystyle C’\). It follows that \(\displaystyle \mathcal{L}\) takes segment \(\displaystyle BB’\) to segment \(\displaystyle CC’\). Hence, triangles \(\displaystyle SBB’,SCC’\) are oppositely similar.
This immediately proves the second part of the problem. By the similarity, we get \(\displaystyle \angle C’SB= \angle CSB'\) and \(\displaystyle BS/B'S=CS/C'S\). Thus,
\(\displaystyle \text{Area}(BC'S)=\dfrac{1}{2}\cdot BS\cdot C'S\cdot\sin \angle BSC'=\dfrac{1}{2}\cdot CS\cdot B'S\cdot\sin \angle B'SC=\text{Area}(CB'S).\)
It remains to prove that \(\displaystyle AK\) passes through \(\displaystyle S\). Luckily, this follows easily from the similarities. Notice that \(\displaystyle K\) is the centre of the spiral similarity taking \(\displaystyle BB'\) to \(\displaystyle C'C\), so
\(\displaystyle \dfrac{d(K,BB')}{d(K,CC')}=\dfrac{d(M,BB')}{d(M,CC')}=\dfrac{|BB'|}{|CC'|}=\dfrac{d(S,BB')}{d(S,CC')}.\)
It is known that the loci of points \(\displaystyle X\) satisfying \(\displaystyle \dfrac{d(X,AB)}{d(X,AC)}=\dfrac{|BB'|}{|CC'|}\) is the union of two lines through \(\displaystyle A\). Clearly, these lines are precisely \(\displaystyle AM\) and \(\displaystyle AK\). Thus, \(\displaystyle S\) must lie on one of them, however, \(\displaystyle S\neq M\) and \(\displaystyle SM\perp AM\), so \(\displaystyle S\in AK\).
It might happen that \(\displaystyle S\) is a point at infinity. Luckily, this doesn't cause any problems for us. The homothety part of \(\displaystyle \mathcal{L}\) becomes a translation and our transformation remains a similarity (in fact, it becomes an isometry). We also note that the choice of \(\displaystyle \mathcal{L}\) is not random, it is called stretch reflection. It can be proved that any orientation reversing similarity is a stretch reflection.
Statistics:
10 students sent a solution. 7 points: Bodor Mátyás, Czanik Pál, Keresztély Zsófia, Szakács Ábel, Varga Boldizsár. 6 points: Forrai Boldizsár, Minh Hoang Tran. 5 points: 1 student. 4 points: 1 student. 1 point: 1 student.
Problems in Mathematics of KöMaL, November 2024
